Xét 4 tế bào sinh tinh ở cơ thể có kiểu gen \[{\rm{Aa}}\frac{{{\rm{BD}}}}{{{\rm{bd}}}}\] giảm phân tạo giao tử. Cho biết các gen liên kết hoàn toàn, trong quá trình giảm phân chỉ có 1 tế bào có cặp NST mang 2 cặp gen B, b và D, d không phân li trong giảm phân I, phân li bình thường trong giảm phân II; cặp NST mang cặp gen A, a phân li bình thường. Kết thúc quá trình giảm phân đã tạo ra 6 loại giao tử, trong đó có 37,5% loại giao tử mang 2 alen trội. Theo lí thuyết, loại giao tử mang 1 alen trội chiếm tỉ lệ là bao nhiêu?
 Giải bởi Vietjack
Giải bởi Vietjack
Kiểu gen \[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\] giảm phân không phân li ở giảm phân I, giảm phân II bình thường sẽ tạo giao tử (\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\]) và giao tử (O). Vậy tế bào sinh tinh giảm phân bị rối loạn sẽ tạo giao tử:
(A, a)(\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\], O) = 2 A\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\] và 2 a hoặc 2 A và 2 a\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\].
Tế bào sinh tinh bình thường tạo giao tử (A, a)(BD, bd) = 2 ABD và 2 abd (kiểu 1) hoặc 2 Abd và 2 aBD (kiểu 2).
Mà 4 tế bào sinh tinh giảm phân được 6 loại giao tử, tức là 4 (bình thường) + 2 (đột biến). Như vậy, với 3 tế bào sinh tinh giảm phân bình thường ta có 2 trường hợp là: 2 tế bào kiểu 1, 1 tế bào kiểu 2 hoặc 1 tế bào kiểu 1, 2 tế bào kiểu 2.
Theo bài ra, 4 tế bào giảm phân thu được 16 giao tử, giao tử 2 alen trội chiếm 3/8 = 6/16.
|
Trường hợp |
ABD |
abd |
aBD |
Abd |
Tỉ lệ 2 trội thiếu |
|
1 tế bào kiểu 1, 2 tế bào kiểu 2 |
2 |
2 |
4 |
4 |
2 |
|
2 tế bào kiểu 1, 1 tế bào kiểu 2 |
4 |
4 |
2 |
2 |
4 (loại) |
Vậy có 1 tế bào giảm phân bình thường kiểu 1, 2 tế bào giảm phân bình thường kiểu 2 và tế bào rối loạn tạo giao tử 2 A và 2 a\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\].
Vậy tỉ lệ giao tử mang 1 alen trội là (4 Abd + 2A)/16 = 6/16 = 37,5%. Đáp án: 37,5%.
Phương trình \({x^3} - 6mx + 5 = 5{m^2}\) có 3 nghiệm phân biệt lập thành cấp số cộng khi
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 2\cos \left( {5t - \frac{\pi }{6}} \right).\) Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hỏi trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho ba điểm \(A\left( {1\,;\,\,0\,;\,\,0} \right),\,\,C\left( {0\,;\,\,0\,;\,\,3} \right),\)\(B\left( {0\,;\,\,2\,;\,\,0} \right).\) Tập hợp các điểm \(M\) thỏa mãn MA2 = MB2 + MC2 là mặt cầu có bán kính là
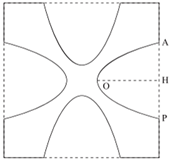
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng \(10\;\,{\rm{cm}}\) bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình vẽ. Biết \(AB = 5\;{\rm{cm}}\,,\,\,OH = 4\;{\rm{cm}}.\) Diện tích bề mặt hoa văn đó là
Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng
Có bao nhiêu số nguyên của \(m\) thuộc đoạn \(\left[ { - 100\,;\,\,100} \right]\) để đồ thị hàm số \(y = \frac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng hai đường tiệm cận?
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Có bao nhiêu giá trị nguyên của \(m\) để giá trị nhỏ nhất của hàm số \[y = \left| {f\left( {2\sin x + 1} \right) + m} \right|\] không vượt quá 10?
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở \[A,\,\,B\] khác tiếp điểm. Độ dài đoạn thẳng \[AB\] là
Cho các phát biểu sau: Các polymer đều có nhiệt độ nóng chảy xác định (1); đa số polymer không tan trong các dung môi thông thường (2); cao su là vật liệu polymer có tính đàn hồi (3); tơ polyamide bền trong môi trường acid và môi trường base (4); tơ visco và tơ acetate thuộc loại tơ hóa học (5). Số phát biểu đúng là
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \(A\left( {2\,;\,\, - 1\,;\,\,1} \right),\)\(B\left( {3\,;\,\,0\,;\,\, - 1} \right),\)\(C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\) và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
Ông Hưng gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất 2,1 một quý trong thời gian 15 tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất \[0,73\% \] một tháng trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai ngân hàng là \[27\,\,507\,\,768,13\] đồng (chưa làm tròn). Hỏi số tiền ông Hưng lần lượt gửi ở hai ngân hàng X và Y là bao nhiêu?
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nhiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?