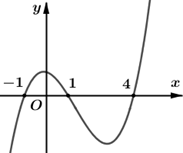
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới đây. Số điểm cực trị của hàm số \(g\left( x \right) = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\) là
Giải bởi Vietjack
Ta có \(g\left( x \right) = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\)
\( \Rightarrow g'\left( x \right) = 2f'\left( x \right) \cdot {e^{2f\left( x \right) + 1}} + f'\left( x \right) \cdot {5^{f\left( x \right)}} \cdot \ln 5 = f'\left( x \right)\left[ {2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}} \cdot \ln 5} \right]\).
Khi đó \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 4\end{array} \right.\) (vì \(2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}} \cdot \ln 5 > 0\,\,\forall x)\).
Qua các điểm \(x = - 1\,,\,\,x = 1\,,\,\,x = 4\) thì \(f'\left( x \right)\) đổi dấu nên \(g'\left( x \right)\) cũng đổi dấu (vì dấu của \(g'\left( x \right)\) phụ thuộc vào dấu của \(f'\left( x \right)\).
Vậy hàm số \(y = g\left( x \right)\) có 3 điểm cực trị. Chọn C.
Cho lăng trụ tam giác \[ABC.A'B'C'\], trên đường thẳng \[BA\] lấy điểm \[M\] sao cho \[A\] nằm giữa \[B\] và \[M\], \(MA = \frac{1}{2}AB,\,\,E\) là trung điểm \[AC.\] Gọi \(D = BC \cap \left( {MB'E} \right)\). Tỉ số \(\frac{{BD}}{{CD}}\) bằng
Đáp án: ……….Gọi \[x,\,\,y,\,\,z\] là chiều dài, chiều rộng và chiều cao của một thùng giấy có dạng hình hộp chữ nhật không có nắp bên trên (hình vẽ). Biết rằng tổng diện tích xung quanh và đáy còn lại của thùng bằng 100 (đơn vị diện tích). Khi chiếc thùng có thể tích lớn nhất thì tổng \({x^2} + {y^2} + {z^2}\) bằng
Đáp án: ……….
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Ngôi chùa mang trong nó bao nhiêu sự tích, bao nhiêu huyền thoại và đã chứng minh bao biến thiên của kinh kì.
