Một nhóm nghiên cứu thực hiện thí nghiệm để kiểm chứng mô hình nhân đôi ADN ở vùng nhân của tế bào nhân sơ. Họ đã nuôi một số vi khuẩn E.coli trong môi trường chỉ có nitơ đồng vị nặng (15N). Sau đó, họ chuyển vi khuẩn sang nuôi tiếp năm thế hệ ở môi trường chỉ có nitơ đồng vị nhẹ (14N). Biết số lần nhân lên của vi khuẩn E.coli trong các ống nghiệm là như nhau. Tách ADN sau mỗi thế hệ và thu được kết quả như hình dưới đây. Cho biết X là vị trí của ADN chứa cả hai mạch 15N; Y là vị trí của ADN chứa cả mạch 14N và mạch 15N; Z là vị trí của ADN chứa cả hai mạch 14N.
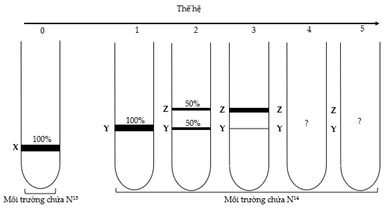
Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I. Thí nghiệm trên đã kiểm chứng quá trình nhân đôi ADN theo nguyên tắc bán bảo toàn.
II. Nếu một vi khuẩn E. coli được nuôi với các điều kiện thí nghiệm như trên thì luôn có hai mạch ADN chứa 15N ở mỗi thế hệ.
III. Ở thế hệ thứ 4, tỉ lệ ADN ở vị trí Y không thay đổi so với thế hệ thứ 3.
IV. Ở thế hệ thứ 5, tỉ lệ ADN ở vị trí Y so với ADN ở vị trí Z là 1/15.
A. 3.
 Giải bởi Vietjack
Giải bởi Vietjack
Giả sử ban đầu có 1 phân tử N15 (X).
- Ở ống nghiệm 1: 1 phân tử X nhân đôi 1 lần trong N14 cho 2 phân tử Y.
- Ở ống nghiệm 2: 2 phân tử Y nhân đôi 1 lần trong N14 cho 2 phân tử Y và 2 phân tử Z.
- Ở ống nghiệm 3:
+ 2 phân tử Y nhân đôi 1 lần trong N14 cho 2 phân tử Y và 2 phân tử Z.
+ 2 phân tử Z nhân đôi 1 lần trong N14 cho 4 phân tử Z.
- Ở ống nghiệm 4:
+ 2 phân tử Y nhân đôi 1 lần trong N14 cho 2 phân tử Y và 2 phân tử Z.
+ 6 phân tử Z nhân đôi 1 lần trong N14 cho 12 phân tử Z.
- Ở ống nghiệm 5:
+ 2 phân tử Y nhân đôi 1 lần trong N14 cho 2 phân tử Y và 2 phân tử Z.
+ 14 phân tử Z nhân đôi 1 lần trong N14 cho 28 phân tử Z.
Xét sự đúng – sai của các phát biểu:
I. Đúng. Thí nghiệm trên đã kiểm chứng quá trình nhân đôi ADN theo nguyên tắc bán bảo toàn.
II. Đúng. Nếu một vi khuẩn E. coli được nuôi với các điều kiện thí nghiệm như trên thì luôn có hai mạch ADN chứa N15 ở mỗi thế hệ (mỗi thế hệ đều có 2 phân tử Y).
III. Sai. Tỉ lệ Y thay đổi từ thế hệ 3 (25%) sang thế hệ 4 (12,5%).
IV. Đúng. Ở thế hệ 5, \(\frac{Y}{Z} = \frac{2}{{30}} = \frac{1}{{15}}.\)
Chọn A.
Cho lăng trụ tam giác \[ABC.A'B'C'\], trên đường thẳng \[BA\] lấy điểm \[M\] sao cho \[A\] nằm giữa \[B\] và \[M\], \(MA = \frac{1}{2}AB,\,\,E\) là trung điểm \[AC.\] Gọi \(D = BC \cap \left( {MB'E} \right)\). Tỉ số \(\frac{{BD}}{{CD}}\) bằng
Đáp án: ……….Tìm \[a\] để hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {4x + 1} - 1}}{{a{x^2} + \left( {2a + 1} \right)x}}{\rm{ khi }}x \ne 0}\\{4\quad {\rm{ khi }}x = 0}\end{array}} \right.\) liên tục tại \(x = 0\).
Đáp án: ……….
Gọi \[x,\,\,y,\,\,z\] là chiều dài, chiều rộng và chiều cao của một thùng giấy có dạng hình hộp chữ nhật không có nắp bên trên (hình vẽ). Biết rằng tổng diện tích xung quanh và đáy còn lại của thùng bằng 100 (đơn vị diện tích). Khi chiếc thùng có thể tích lớn nhất thì tổng \({x^2} + {y^2} + {z^2}\) bằng
Đáp án: ……….
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Ngôi chùa mang trong nó bao nhiêu sự tích, bao nhiêu huyền thoại và đã chứng minh bao biến thiên của kinh kì.