Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Nam Cao là nhà văn hiện thực lớn, một nhà nhân đạo chủ nghĩa lớn. Ông có nhiều đóng góp quan trọng đối với việc hoàn thiện truyện ngắn và tiểu thuyết Việt Nam trên quá trình _________ ở nửa đầu thế kỉ XX.
A. thi vị hóa.
 Giải bởi Vietjack
Giải bởi Vietjack
Hiện đại hóa được hiểu là quá trình làm cho văn học thoát ra khỏi hệ thống thi pháp văn học trung đại và đổi mới theo hình thức của văn học phương Tây, có thể hội nhập với nền văn học trên thế giới. Đầu thế kỉ XX, thực dân Pháp xâm lược và đẩy mạnh công cuộc khai thác thuộc địa, làm cho xã hội nước ta có nhiều thay đổi: xuất hiện nhiều đô thị và nhiều tầng lớp mới, nhu cầu thẩm mĩ cũng thay đổi. Từ đó, nền văn học dần thoát khỏi sự ảnh hưởng của văn học Trung Hoa và dần hội nhập với nền văn học Phương Tây mà cụ thể là nền văn học nước Pháp. Chọn B.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
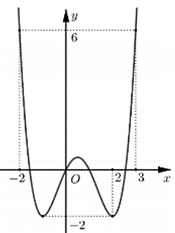
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
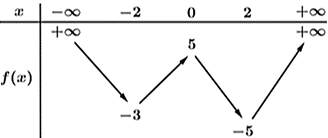
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
Cho biểu đồ:
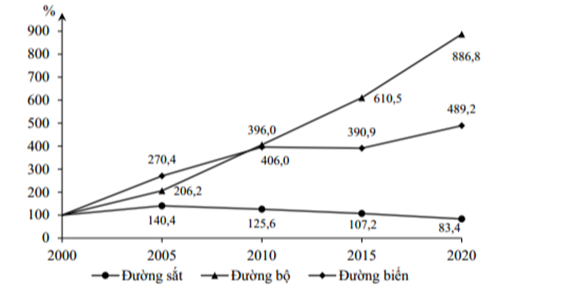
KHỐI LƯỢNG HÀNG HÓA VẬN CHUYỂN
MỘT SỐ NGÀNH VẬN TẢI NƯỚC TA GIAI ĐOẠN 2000-2020
(Nguồn: Niên giám Thống kê Việt Nam năm 2020, NXB Thống kê, 2021)
Biểu đồ thể hiện nội dung nào sau đây?