Đọc đoạn trích sau đây và trả lời câu hỏi:
Trong rừng, anh Quyết dạy Tnú và Mai học chữ. Anh chẻ nứa, đập giập, ghép lại thành mấy tấm bảng to bằng ba bàn tay. Ba anh em đốt khói xà nu xông bảng nứa đen kịt rồi lấy nhựa cây luông tờ ngheo phết lên một lớp dày, rửa nước cũng không phai được. Tnú đi ba ngày đường tới núi Ngọc Linh mang về một xà lét đầy đá trắng làm phấn. Mai học giỏi hơn Tnú, ba tháng đọc được chữ, viết được cái ý trong bụng mình muốn, sáu tháng làm được toán hai con số. Tnú học chậm hơn, mà lại hay nổi nóng. Học tới chữ i dài, nó quên mất chữ o thêm cái móc thì đọc được là chữ a. Có lần thua Mai, nó đập bể cả cái bảng nứa trước mặt Mai và anh Quyết, bỏ ra suối ngồi một mình suốt ngày. Anh Quyết ra dỗ, nó không nói. Mai ra dỗ, nó đòi đánh Mai. Mai cũng ngồi lì đó với nó:
– Tnú không về, tui cũng không về. Về đi, anh Tnú. Mai làm cái bảng khác cho anh rồi.
Nó cầm một hòn đá, tự đập vào đầu, chảy máu ròng ròng. Anh Quyết phải băng lại cho nó. Đêm đó, anh ôm nó trong hốc đá. Anh rủ rỉ:
– Sau này, nếu Mĩ - Diệm giết anh, Tnú phải làm cán bộ thay anh. Không học chữ sao làm được cán bộ giỏi? Tnú giả ngủ không nghe. Nó lén chùi nước mắt giàn giụa. Sáng hôm sau, nó gọi Mai ra sau hốc đá:
– Mai nói cho tôi chữ o có móc là chữ chi đi. Còn chữ chi đứng sau chữ đó nữa, chữ chi có cái bụng to đó.
(Rừng xà nu – Nguyễn Trung Thành)
 Giải bởi Vietjack
Giải bởi Vietjack
Đoạn trích thể hiện tính cách giàu lòng tự trọng và ý chí quyết tâm của nhân vật Tnú. Chọn A.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
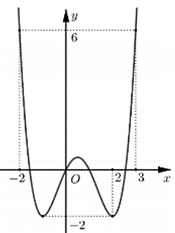
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
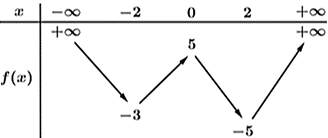
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?
Cho biểu đồ:
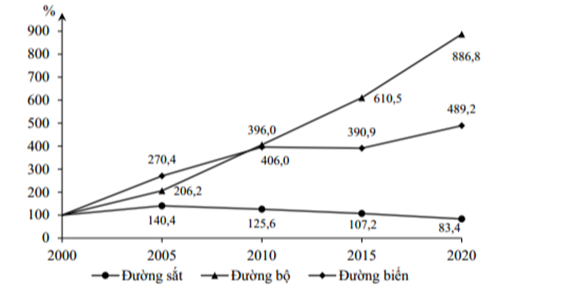
KHỐI LƯỢNG HÀNG HÓA VẬN CHUYỂN
MỘT SỐ NGÀNH VẬN TẢI NƯỚC TA GIAI ĐOẠN 2000-2020
(Nguồn: Niên giám Thống kê Việt Nam năm 2020, NXB Thống kê, 2021)
Biểu đồ thể hiện nội dung nào sau đây?