Đọc đoạn trích sau đây và trả lời câu hỏi:
Hồn Trương Ba: (sau một lát) Ông Đế Thích ạ, tôi không thể tiếp tục mang thân anh hàng thịt được nữa, không thể được!
Đế Thích: Sao thế? Có gì không ổn đâu!
Hồn Trương Ba: Không thể bên trong một đằng, bên ngoài một nẻo được. Tôi muốn được là tôi toàn vẹn.
Đế Thích: Thế ông ngỡ tất cả mọi người đều được là mình toàn vẹn ư? Ngay cả tôi đây. Ở bên ngoài, tôi đâu có được sống theo những điều tôi nghĩ bên trong. Mà cả Ngọc Hoàng nữa, chính người lắm khi cũng phải khuôn ép mình cho xứng với danh vị Ngọc Hoàng. Dưới đất, trên trời đều thế cả, nữa là ông. Ông bị gạch tên khỏi sổ Nam Tào. Thân thể thật của ông đã tan rữa trong bùn đất, còn chút hình thù gì của ông đâu!
Hồn Trương Ba: Sống nhờ vào đồ đạc, của cải người khác, đã là chuyện không nên, đằng này đến cái thân tôi cũng phải sống nhờ anh hàng thịt. Ông chỉ nghĩ đơn giản là cho tôi sống, nhưng sống như thế nào thì ông chẳng cần biết!
(Trích Hồn Trương Ba da hàng thịt – Lưu Quang Vũ)
 Giải bởi Vietjack
Giải bởi Vietjack
. Đoạn trích được viết theo thể loại kịch. Chọn C.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
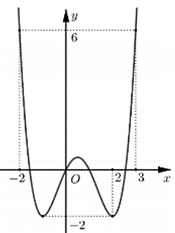
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
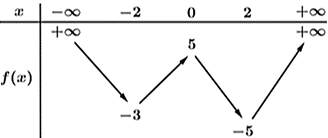
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
Cho biểu đồ:
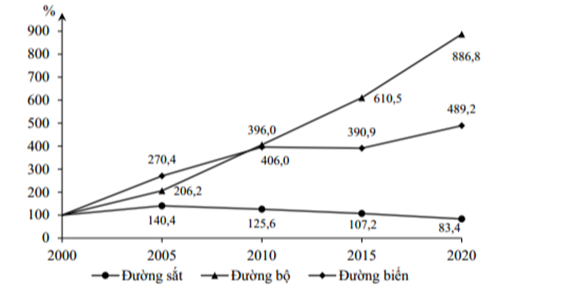
KHỐI LƯỢNG HÀNG HÓA VẬN CHUYỂN
MỘT SỐ NGÀNH VẬN TẢI NƯỚC TA GIAI ĐOẠN 2000-2020
(Nguồn: Niên giám Thống kê Việt Nam năm 2020, NXB Thống kê, 2021)
Biểu đồ thể hiện nội dung nào sau đây?