Đọc đoạn trích sau và trả lời câu hỏi:
Hắn vừa đi vừa chửi. Bao giờ cũng thế, cứ rượu xong là hắn chửi. Bắt đầu hắn chửi trời. Có hề gì? Trời có của riêng nhà nào? Rồi hắn chửi đời. Thế cũng chẳng sao: đời là tất cả nhưng chẳng là ai. Tức mình, hắn chửi ngay tất cả làng Vũ Đại. Nhưng cả làng Vũ Đại ai cũng nhủ: “Chắc nó trừ mình ra!”. Không ai lên tiếng cả. Tức thật! Ờ! Thế này thì tức thật! Tức chết đi được mất! Đã thế, hắn phải chửi cha đứa nào không chửi nhau với hắn. Nhưng cũng không ai ra điều. Mẹ kiếp! Thế có phí rượu không? Thế thì có khổ hắn không? Không biết đứa chết mẹ nào lại đẻ ra thân hắn cho hắn khổ đến nông nỗi này? A ha! Phải đấy hắn cứ thế mà chửi, hắn cứ chửi đứa chết mẹ nào đẻ ra thân hắn, đẻ ra cái thằng Chí Phèo! Hắn nghiến răng vào mà chửi cái đứa đã đẻ ra Chí Phèo. Nhưng mà biết đứa nào đã đẻ ra Chí Phèo? Có mà trời biết! Hắn không biết, cả làng Vũ Đại cũng không ai biết...
(Chí Phèo – Nam Cao)
 Giải bởi Vietjack
Giải bởi Vietjack
Điệp cú pháp: Hắn vừa đi vừa chửi. Bao giờ cũng thế, cứ rượu xong là hắn chửi. Bắt đầu hắn chửi trời. Có hề gì? Trời có của riêng nhà nào? Rồi hắn chửi đời. Thế cũng chẳng sao: đời là tất cả nhưng chẳng là ai… Thế có phí rượu không? Thế thì có khổ hắn không?
Liệt kê: chửi trời, chửi đời, chửi cả làng Vũ Đại, chửi cha đứa nào không chửi nhau với hắn, chửi đứa chết mẹ nào đẻ ra thân hắn,…
Câu hỏi tu từ: Không biết đứa chết mẹ nào lại đẻ ra thân hắn cho hắn khổ đến nông nỗi này? Nhưng mà biết đứa nào đã đẻ ra Chí Phèo?....
→ Chọn A.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
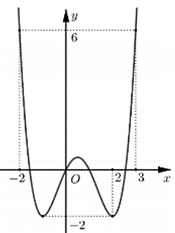
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
Cho biểu đồ:
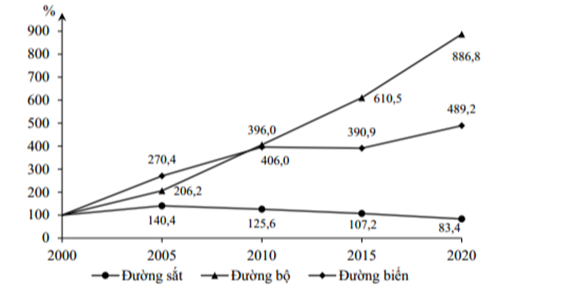
KHỐI LƯỢNG HÀNG HÓA VẬN CHUYỂN
MỘT SỐ NGÀNH VẬN TẢI NƯỚC TA GIAI ĐOẠN 2000-2020
(Nguồn: Niên giám Thống kê Việt Nam năm 2020, NXB Thống kê, 2021)
Biểu đồ thể hiện nội dung nào sau đây?
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
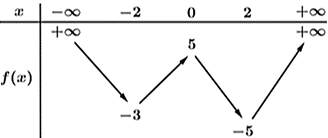
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?
Trong một hộp có 100 tấm thẻ được đánh số từ 101 đến 200 (mỗi tấm thẻ được đánh một số khác nhau). Lấy ngẫu nhiên đồng thời 3 tấm thẻ trong hộp. Xác suất để tổng các số ghi trên 3 tấm thẻ đó là một số chia hết cho 3 là