Cho hai hàm số \(y =  - 2{x^2}\) và \(y =  - 2x - 4.\)

1) Vẽ đồ thị các hàm số này trên cùng một mặt phẳng tọa độ.

2) Tìm tọa độ hai giao điểm \(C,\,\,D\) của hai đồ thị đó. Tính khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(CD.\)

1) ⦁ Vẽ đồ thị hàm số \(y =  - 2{x^2}.\)

Ta có bảng giá trị của \(y\) tương ứng với giá trị của \(x\) như sau:

\(x\)	\[--2\]	\[--1\]	\[0\]	\[1\]	\[2\]
\(y =  - 2{x^2}\)	\( - 8\)	\( - 2\)	\[0\]	\( - 2\)	\( - 8\)

 

 

 

Vẽ các điểm \(\left( { - 2; - 8} \right),\) \(\left( { - 1; - 2} \right),\) \(\left( {0;0} \right),\) \(\left( {1; - 2} \right),\) \(\left( {2; - 8} \right)\) thuộc đồ thị của hàm số \(y =  - 2{x^2}\) trong mặt phẳng tọa độ \(Oxy.\)

Vẽ đường parabol đi qua năm điểm trên, ta nhận được đồ thị hàm số \(y =  - 2{x^2}\) (hình vẽ).

⦁ Vẽ đồ thị hàm số \(y =  - 2x - 4.\)

Cho \(x = 0\) ta có \(y =  - 4.\) Đồ thị hàm số đi qua điểm \(A\left( {0; - 4} \right).\)

Đồ thị của hàm số \(y =  - 2{x^2}\) và \(y =  - 2x - 4\) trên cùng một mặt phẳng tọa độ:

Cho \(y = 0\) ta có \(x =  - 2.\) Đồ thị hàm số đi qua điểm \(B\left( { - 2;0} \right).\)

Vẽ đường thẳng đi qua hai điểm \(A\left( {0; - 4} \right)\) và \(B\left( { - 2;0} \right)\) ta được đồ thị hàm số \(y =  - 2x - 4\) (hình vẽ).

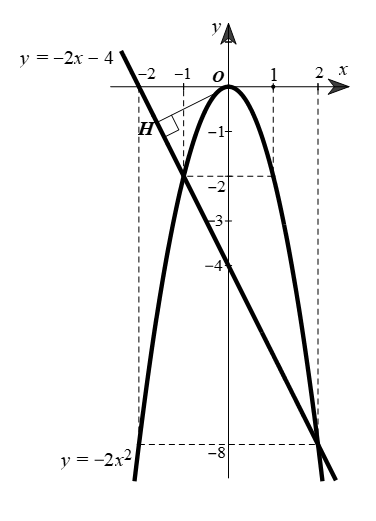
2) ⦁ Gọi \(\left( {{x_0};{y_0}} \right)\) là tọa độ giao điểm (nếu có) của hai đồ thị hàm số \(y =  - 2x - 4\) và \(y =  - 2{x^2},\) khi đó ta có:    \({y_0} =  - 2{x_0} - 4\) và \({y_0} =  - 2x_0^2.\)

Suy ra \( - 2{x_0} - 4 =  - 2x_0^2\) hay \(x_0^2 - {x_0} - 2 = 0.\)

Số giao điểm của hai đồ thị là số nghiệm của phương trình \(x_0^2 - {x_0} - 2 = 0.\,\,\,\left( 1 \right)\)

Ta có: \(a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên phương trình \(\left( 1 \right)\) có hai nghiệm là \({x_0} =  - 1\) và \({x_0} = 2.\)

Với \({x_0} =  - 1,\) ta có \({y_0} =  - 2 \cdot \left( { - 1} \right) - 4 =  - 2;\)

Với \({x_0} = 2,\) ta có \({y_0} =  - 2 \cdot 2 - 4 =  - 8.\)

Vậy tọa độ giao điểm \(C,\,\,D\) của hai đồ thị là: \(C\left( { - 1; - 2} \right)\) và \(D\left( {2; - 8} \right),\) hoặc \(C\left( {2; - 8} \right)\) và \(D\left( { - 1; - 2} \right).\)

⦁ Khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(CD\) chính là khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(y =  - 2x - 4.\)

Gọi \(H\) là chân đường cao kẻ từ \(O\) xuống đường thẳng \[CD,\] ta có \(OH \bot CD.\)

Ta có \(A\left( {0; - 4} \right),\,\,B\left( { - 2;0} \right)\) suy ra \(OA = 4,\,\,OB = 2.\)

Xét \(\Delta OAB\) vuông tại \(O,\) có:

⦁ \(A{B^2} = O{A^2} + O{B^2}\) (định lí Pythagore)

Suy ra \(AB = \sqrt {O{A^2} + O{B^2}}  = \sqrt {{4^2} + {2^2}}  = \sqrt {20}  = 2\sqrt 5 .\)

⦁ \(\sin \widehat {OBA} = \frac{{OA}}{{AB}}.\)

Xét \(\Delta OBH\) vuông tại \(H,\) có: \(\sin \widehat {OBH} = \frac{{OH}}{{OB}}.\)

Suy ra \(\frac{{OA}}{{AB}} = \frac{{OH}}{{OB}},\) do đó \(OH = \frac{{OA \cdot OB}}{{AB}} = \frac{{4 \cdot 2}}{{2\sqrt 5 }} = \frac{{4\sqrt 5 }}{5}.\)

Vậy khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(CD\) bằng \(\frac{{4\sqrt 5 }}{5}.\)