Giải bởi Vietjack
Giải bởi Vietjack
Gọi \(x(\;{\rm{cm}})\) là độ dài cạnh hình lập phương ban đầu, ta có \({(3{\rm{x}})^3} - {{\rm{x}}^3} = 208 \Rightarrow {\rm{x}} = 2(\;{\rm{cm}}).\)
Chọn B.
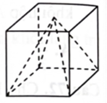
Tỉ số của thể tích khối chóp có đỉnh thuộc mặt đáy và khối hộp như hình vẽ bên là