Giải bởi Vietjack
Giải bởi Vietjack
\({\rm{S}} = (6 + 8 + 10) \cdot 10 + 2 \cdot \frac{1}{2} \cdot 6 \cdot 8 = 288\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\) Chọn A.
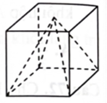
Tỉ số của thể tích khối chóp có đỉnh thuộc mặt đáy và khối hộp như hình vẽ bên là