Hai bạn An và Bình chơi một trò chơi qua hai vòng. Ở vòng một, cứ mỗi lượt chơi ai thắng thì được 3 điểm, còn thua thì bị trừ 1 điểm. Ở vòng thứ hai, cứ mỗi lượt chơi, ai thắng thì lại được 4 điểm, còn thua thì bị trừ 2 điểm. Biết rằng sau khi chơi xong thì tổng điểm của hai bạn là 56 và An nhiều điểm hơn Bình. Giả sử rằng An đã thắng tất cả các trận ở vòng một nhưng lại thua tất cả các trận ở vòng hai. Hỏi ở vòng một có ít nhất bao nhiêu trận (nhập đáp án vào ô trống)?
![]()
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x, y lần lượt là số trận của vòng 1 và 2, trong đó ![]() nguyên dương.
nguyên dương.
Theo giả thiết thì số điểm của A là 3x – 2y, số điểm của B là ![]() .
.
Theo đề ta có: ![]() .
.
Suy ra tổng số trận là 28.
Ta có điểm của An nhiều hơn của Bình nên 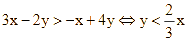 .
.
Có 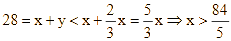 . Mà x nguyên dương nên x = 17.
. Mà x nguyên dương nên x = 17.
Do đó vòng 1 có ít nhất 17 trận.
Đáp án cần nhập là: 17.
Đọc đoạn trích sau và trả lời câu hỏi:
Bạn không nên để thất bại ngăn mình tiến về phía trước. Hãy suy nghĩ tích cực về thất bại và rút ra kinh nghiệm. Thực tế những người thành công luôn dùng thất bại như là một công cụ để học hỏi và hoàn thiện bản thân. Họ có thể nghi ngờ phương pháp làm việc đã dẫn họ đến thất bại nhưng không bao giờ nghi ngờ khả năng của chính mình.
Nhận xét về cách thức trình bày đoạn văn trên:
Enthalpy tạo thành chuẩn của một chất (![]() ) là biến thiên enthalpy của phản ứng tạo thành 1 mol chất đó từ các đơn chất ở dạng bền nhất trong điều kiện chuẩn. Nhiệt dung riêng của một chất là nhiệt lượng cần cung cấp để 1 kg chất đó tăng lên
) là biến thiên enthalpy của phản ứng tạo thành 1 mol chất đó từ các đơn chất ở dạng bền nhất trong điều kiện chuẩn. Nhiệt dung riêng của một chất là nhiệt lượng cần cung cấp để 1 kg chất đó tăng lên ![]()
Cho phản ứng nhiệt nhôm:
2Al(s) + ![]() (s)
(s) ![]()
![]() (s) + 2Fe(s)
(s) + 2Fe(s)
Biết nhiệt tạo thành, nhiệt dung của các chất được cho trong bảng sau:
|
Chất |
|
C (J/g.K) |
Chất |
|
C (J/g.K) |
|
Al |
0 |
|
|
−16,37 |
0,84 |
|
|
−5,14 |
|
Fe |
0 |
0,67 |
Giả thiết phản ứng xảy ra vừa đủ, hiệu suất 100%; nhiệt độ ban đầu là ![]() , nhiệt lượng toả ra bị thất thoát ra ngoài môi trường là 50%. Nhiệt độ đạt được trong lò phản ứng nhiệt nhôm là
, nhiệt lượng toả ra bị thất thoát ra ngoài môi trường là 50%. Nhiệt độ đạt được trong lò phản ứng nhiệt nhôm là
Đọc đoạn trích sau và trả lời câu hỏi:
Mưa đổ bụi êm êm trên bến vắng,
Đò biếng lười nằm mặc nước sông trôi;
Quán tranh đứng im lìm trong vắng lặng
Bên chòm xoan hoa tím rụng tơi bời
Ngoài đường đê cỏ non tràn biếc cỏ,
Đàn sáo đen sà xuống mổ vu vơ
Mấy cánh bướm rập rờn trôi trước gió.
Những trâu bò thong thả cúi ăn mưa.
(Chiều xuân – Anh Thơ)
Nội dung chính của bức tranh chiều xuân là gì?
Ở ruồi giấm, allele A quy định thân xám trội hoàn toàn so với allele a quy định thân đen; allele B quy định cánh dài trội hoàn toàn so với allele b quy định cánh cụt; 2 cặp gene này nằm trên NST thường; allele D quy định mắt đỏ trội hoàn toàn so với allele d quy định mắt trắng, cặp gene này nằm ở vùng không tương đồng trên NST giới tính X. Phép lai P dị hợp 3 cặp gene: Ruồi thân xám, cánh dài, mắt đỏ × Ruồi thân xám, cánh dài, mắt đỏ, thu được F1 có 17,5% ruồi thân xám, cánh dài, mắt trắng. Theo lí thuyết, trong tổng số ruồi cái thân xám, cánh dài, mắt đỏ ở F1, số ruồi không thuần chủng chiếm tỉ lệ là bao nhiêu (nhập đáp án vào ô trống)?
Đáp án: _______.
Cho hàm số 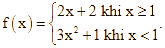 Giả sử
Giả sử ![]() là một nguyên hàm của
là một nguyên hàm của ![]() thoả mãn
thoả mãn ![]() Giá trị của
Giá trị của ![]() bằng (nhập đáp án vào ô trống):
bằng (nhập đáp án vào ô trống):
![]()
Người ta dùng bơm có pit-tông diện tích 8 cm2 và khoảng chạy 25 cm để bơm một bánh xe đạp sao cho khi áp lực của bánh lên mặt đường là 350 N thì diện tích tiếp xúc của bánh với mặt đường là 50 cm2. Ban đầu bánh chứa không khí có áp suất p0 = 105 Pa và thể tích V0 = 1 500 cm3. Giả thiết khi áp suất không khí trong bánh vượt quá 1,5p0 thì thể tích trong của xăm là 2 000 cm3 và nhiệt độ không khí trong xăm không đổi. Phải đẩy bơm tối thiểu bao nhiêu lần (nhập đáp án vào ô trống, làm tròn đến hàng đơn vị).
![]()
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn ![]() của tham số
của tham số ![]() để đường thẳng
để đường thẳng ![]() cắt đồ thị hàm số
cắt đồ thị hàm số ![]() tại hai điểm phân biệt (nhập đáp án vào ô trống)?
tại hai điểm phân biệt (nhập đáp án vào ô trống)?
![]()