Cho đường tròn tâm \[O\] bán kính \[4{\rm{\;cm}}\] và một điểm \[A\] cách \[O\] là \[7{\rm{\;cm}}.\] Kẻ tiếp tuyến \[AB\] với đường tròn (điểm \[B\] là tiếp điểm). Khi đó độ dài \[AB\] là
A. \[AB = 3{\rm{\;cm}}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
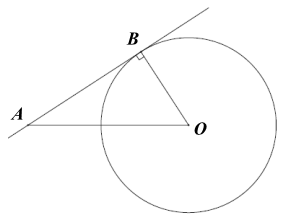
Vì \[AB\] là tiếp tuyến của đường tròn \[\left( O \right),\] với \[B\] là tiếp điểm nên \[AB \bot OB\] tại \[B.\]
Áp dụng định lí Pythagore cho tam giác \[OAB\] vuông tại \[B,\] ta được: \[O{A^2} = O{B^2} + A{B^2}.\]
Suy ra \[A{B^2} = O{A^2} - O{B^2} = {7^2} - {4^2} = 33.\] Do đó \[AB = \sqrt {33} {\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án C.
Hai tiếp tuyến tại \[A\] và \[B\] của đường tròn \[\left( O \right)\] cắt nhau tại \[I.\] Đường thẳng qua \[I\] vuông góc với \[IA\] cắt \[OB\] tại \[K.\] Khẳng định nào sau đây là đúng?
I. Nhận biết
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung?
Cho đường tròn \[\left( O \right)\] và đường thẳng \[a.\] Kẻ \[OH \bot a\] tại điểm \[H,\] biết \[OH > R.\] Khi đó, đường thẳng \[a\] và đường tròn \[\left( O \right)\] có vị trí tương đối là
Cho \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[2,5{\rm{\;cm}}.\] Lấy điểm \[I\] trên \[a\] và vẽ đường tròn \[\left( {I;2,5{\rm{\;cm}}} \right).\] Khi đó đường tròn \[\left( I \right)\] với đường thẳng \[b\]
Hai tiếp tuyến tại \(B\) và \(C\) của đường tròn \(\left( O \right)\) cắt nhau tại \(A.\) Biết \(OB = 3{\rm{\;cm}},\,\,OA = 5{\rm{\;cm}}{\rm{.}}\) Khẳng định nào sau đây là sai?
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Khẳng định nào sau đây là đúng?
II. Thông hiểu
Cho \[a\] và \[b\] là hai đường thẳng song song và cách nhau một khoảng bằng \[3{\rm{\;cm}}.\] Lấy điểm \[I\] trên \[a\] và vẽ đường tròn \[\left( {I;3,5{\rm{\;cm}}} \right).\] Khi đó đường tròn \[\left( I \right)\] với đường thẳng \[b\]
Cho đường tròn \[\left( O \right),\] bán kính \[R = OA,\] dây \[CD\] là đường trung trực của \[OA.\] Kẻ tiếp tuyến với đường tròn tại \[C,\] tiếp tuyến này cắt đường thẳng \[OA\] tại \[I.\] Cho các khẳng định sau:
(i) Tứ giác \[CODA\] là hình thoi.
(ii) \[CI = R\sqrt 3 .\]
Kết luận nào sau đây đúng nhất?
Cho đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và một điểm \[A\] nằm ngoài \[\left( O \right).\] Qua \[A,\] kẻ đường thẳng cắt đường tròn \[\left( O \right)\] tại hai điểm \[B\] và \[C\] (điểm \[B\] nằm giữa hai điểm \[A\] và \[C)\] sao cho \[AB = BC.\] Vẽ đường kính \[CD\] của đường tròn \[\left( O \right).\] Khi đó độ dài đoạn \[AD\] bằng
Cho đường tròn \[\left( {O;R} \right)\] và dây \[AB = 1,2R.\] Vẽ một tiếp tuyến song song với \[AB,\] cắt các tia \[OA,OB\] lần lượt tại \[E\] và \[F.\] Diện tích tam giác \[OEF\] theo \[R\] là
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] và điểm \[A\] nằm ngoài \[\left( O \right).\] Từ \[A\] kẻ hai tiếp tuyến \[AB,AC\] với đường tròn \[\left( O \right)\] (hai điểm \[B,C\] là các tiếp điểm). Gọi \[H\] là giao điểm của \[OA\] và \[BC.\] Lấy \[D\] đối xứng với \[B\] qua \[O.\] Gọi \[E\] là giao điểm của đoạn thẳng \[AD\] với đường tròn \[\left( O \right)\] (điểm \[E\] khác điểm \[D\]) . Tỉ số \[\frac{{DE}}{{BE}}\] bằng
Cho đường tròn \[\left( O \right),\] từ một điểm \[M\] ở ngoài \[\left( O \right),\] vẽ hai tiếp tuyến \[MA\] và \[MB\] sao cho \[\widehat {AMB}\] bằng \[120^\circ .\] Biết chu vi tam giác \[MAB\] là \[6\left( {3 + 2\sqrt 3 } \right){\rm{\;cm}}.\] Khi đó độ dài dây \[AB\] bằng
Cho đường tròn \[\left( O \right)\] và đường thẳng \[a.\] Kẻ \[OH \bot a\] tại điểm \[H,\] biết \[OH < R.\] Khi đó, đường thẳng \[a\] và đường tròn \[\left( O \right)\]