Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường
A. trung trực.
B. đường cao.
C. phân giác ngoài.
D. phân giác trong.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của tam giác đó.
Cho \[\left( {O;{\rm{ }}4} \right)\] có dây \[AC\] bằng cạnh hình vuông nội tiếp và dây \[BC\] bằng cạnh tam giác đều nội tiếp đường tròn đó (điểm \[C\] và \[A\] nằm cùng phía với \[BO\]). Số đo góc \[ACB\] là
Cho tam giác \[ABC\] có \[AB = 6\,\,{\rm{cm}}\]; \[BC = 10{\rm{ cm}}\] và \[AC = 8\,\,{\rm{cm}}\]. Bán kính đường tròn ngoại tiếp tam giác \[ABC\] là
Độ dài cạnh của tam giác đều nội tiếp \[\left( {O;{\rm{ }}R} \right)\] theo \[R\] là
III. Vận dụng
Cho \[\Delta ABC\] vuông tại \[A\], \(\widehat {BAC} = 90^\circ \,\,\left( {AB{\rm{ }} \le {\rm{ }}AC} \right)\). Đường tròn \[\left( I \right)\] nội tiếp tam giác \[ABC\] tiếp xúc với \[BC\] tại \[D\]. Kết quả nào sau đây là đúng?
Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 6 cm và 4 cm (như hình vẽ).
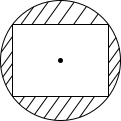
Diện tích phần bị gạch chéo là bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
II. Thông hiểu
Đường tròn nội tiếp hình vuông cạnh \[a\] có bán kính là
Diện tích tam giác đều nội tiếp đường tròn \(\left( {O\,;\,\,2\,\,{\rm{cm}}} \right)\) là
Cho tam giác \[ABC\] vuông tại \[A\], có \[AB = 5\,\,{\rm{cm}}\]; \[AC = 12\,\,{\rm{cm}}\]. Bán kính đường tròn ngoại tiếp tam giác \[ABC\] là
Cho \[\Delta ABC\] vuông tại \[A\], có \[AB = 6{\rm{ cm}}\] và \[AC = 8{\rm{ cm}}\] ngoại tiếp đường tròn \[\left( {I;{\rm{ }}r} \right)\]. Bán kính \[r\] của đường tròn là
Tam giác \[ABC\] vuông tại \[A\] có đường cao \[AH = \frac{{12}}{5}\] cm và \(\frac{{AB}}{{AC}} = \frac{3}{4}\). Bán kính \[R\] của đường tròn ngoại tiếp tam giác \[ABC\] là