Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 6 cm và 4 cm (như hình vẽ).
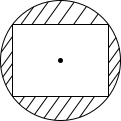
Diện tích phần bị gạch chéo là bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
A. \[16,12{\rm{ c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
B. \[16,84{\rm{ c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
C. \[{\rm{24,15 c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
D. \[{\rm{24,05 c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Áp dụng định lí Pythagore, ta có độ dài đường chéo của hình chữ nhật là:
\[\sqrt {{6^2} + {4^2}} = \sqrt {52} = 2\sqrt {13} \] (cm).
Hình chữ nhật nội tiếp đường tròn nên đường kính của đường tròn chính là độ dài của đường chéo hình chữ nhật.
Bán kính đường tròn là: \[R = \frac{{2\sqrt {13} }}{2} = \sqrt {13} \] (cm).
Diện tích hình chữ nhật là: \[{S_{hcn}} = 6 \cdot 4 = 24{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right){\rm{.}}\]
Diện tích hình tròn là: \[{S_{h\`i nh{\rm{ }}tr\`o n}} = \pi {R^2} = 13\pi {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right){\rm{.}}\]
Diện tích phần bị gạch chéo là: \[S = {S_{tr\`o n}}--{S_{hcn}} = 13\pi --24 \approx 16,84{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right).\]
Vậy diện tích phần bị gạch chéo bằng khoảng \[16,84{\rm{ c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
II. Thông hiểu
Đường tròn nội tiếp hình vuông cạnh \[a\] có bán kính là
Cho \[\left( {O;{\rm{ }}4} \right)\] có dây \[AC\] bằng cạnh hình vuông nội tiếp và dây \[BC\] bằng cạnh tam giác đều nội tiếp đường tròn đó (điểm \[C\] và \[A\] nằm cùng phía với \[BO\]). Số đo góc \[ACB\] là
Cho tam giác \[ABC\] có \[AB = 6\,\,{\rm{cm}}\]; \[BC = 10{\rm{ cm}}\] và \[AC = 8\,\,{\rm{cm}}\]. Bán kính đường tròn ngoại tiếp tam giác \[ABC\] là
Diện tích tam giác đều nội tiếp đường tròn \(\left( {O\,;\,\,2\,\,{\rm{cm}}} \right)\) là
III. Vận dụng
Cho \[\Delta ABC\] vuông tại \[A\], \(\widehat {BAC} = 90^\circ \,\,\left( {AB{\rm{ }} \le {\rm{ }}AC} \right)\). Đường tròn \[\left( I \right)\] nội tiếp tam giác \[ABC\] tiếp xúc với \[BC\] tại \[D\]. Kết quả nào sau đây là đúng?
Độ dài cạnh của tam giác đều nội tiếp \[\left( {O;{\rm{ }}R} \right)\] theo \[R\] là
Cho tam giác \[ABC\] vuông tại \[A\], có \[AB = 5\,\,{\rm{cm}}\]; \[AC = 12\,\,{\rm{cm}}\]. Bán kính đường tròn ngoại tiếp tam giác \[ABC\] là
Cho \[\Delta ABC\] vuông tại \[A\], có \[AB = 6{\rm{ cm}}\] và \[AC = 8{\rm{ cm}}\] ngoại tiếp đường tròn \[\left( {I;{\rm{ }}r} \right)\]. Bán kính \[r\] của đường tròn là
Tam giác \[ABC\] vuông tại \[A\] có đường cao \[AH = \frac{{12}}{5}\] cm và \(\frac{{AB}}{{AC}} = \frac{3}{4}\). Bán kính \[R\] của đường tròn ngoại tiếp tam giác \[ABC\] là