Cho ngũ giác đều \[ABCDE\]. Khẳng định nào sau đây là sai?
A. Ngũ giác đều\[ABCDE\] có một tâm đối xứng.
B. Mỗi góc trong của ngũ giác đều \[ABCDE\] là \(108^\circ \).
C. Tổng các góc trong của ngũ giác đều \[ABCDE\] là \(450^\circ \).
D. Tổng các góc trong của ngũ giác đều \[ABCDE\] là \(540^\circ \).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Tổng các góc trong của một ngũ giác đều là:
\(180^\circ \left( {5 - 2} \right) = 540^\circ \).
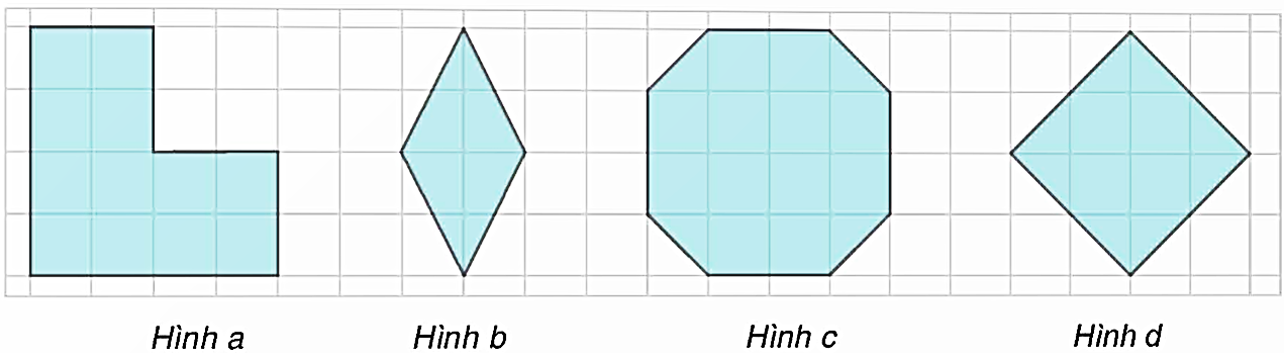
Trong các hình phẳng sau, các hình là hình phẳng có dạng là đa giác đều là:
Mỗi góc của lục giác đều nội tiếp đường tròn tâm \[O\] có số đo là:
Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là \(5{\rm{ cm}}\). Chu vi đa giác đều này là
Cho đa giác đều 9 cạnh có tâm \[O\] và \[AB,{\rm{ }}BC\] là hai cạnh của đa giác (như hình vẽ).
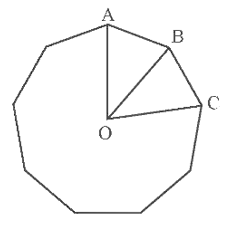
Số đo các góc \[\widehat {AOB}\,,\,\,\widehat {ABO}\,,\,\,\widehat {ABC}\] lần lượt là
Một lục giác đều và một ngũ giác đều chung cạnh \[AD\] (như hình vẽ).
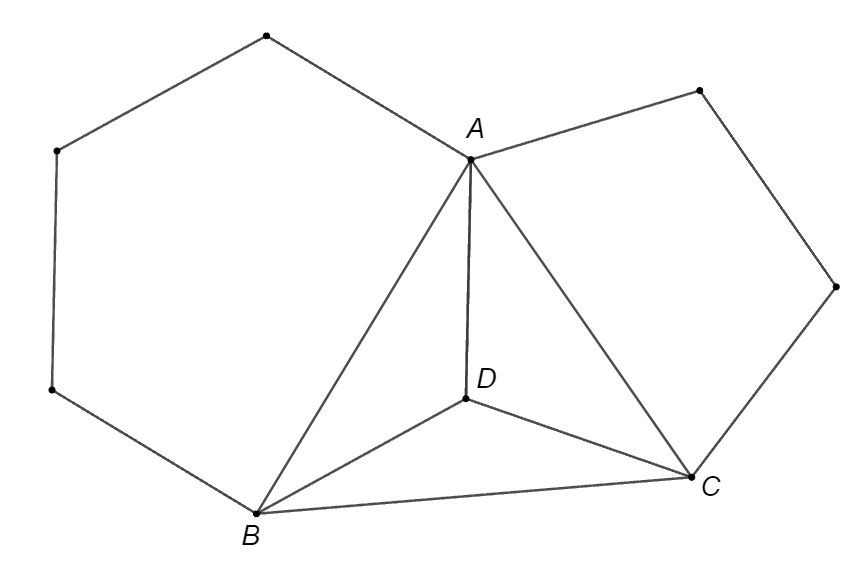
Số đo góc \(BAC\) là
I. Nhận biết
Cho các hình dưới đây:
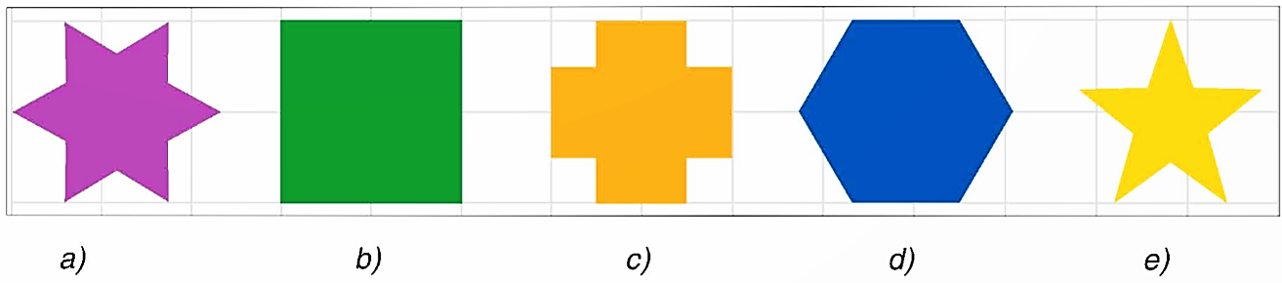
Trong các hình trên, hình nào có dạng là đa giác đều?
Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.
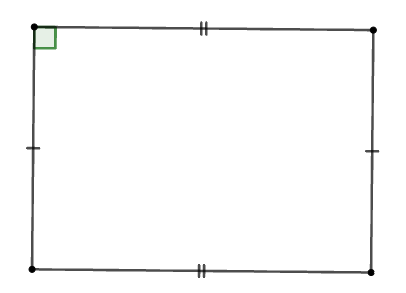
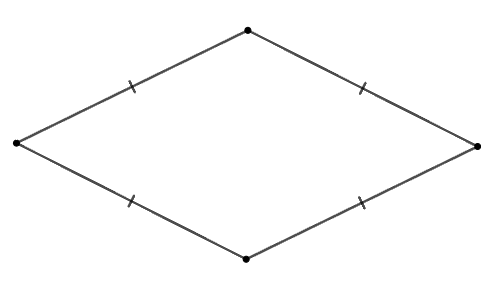
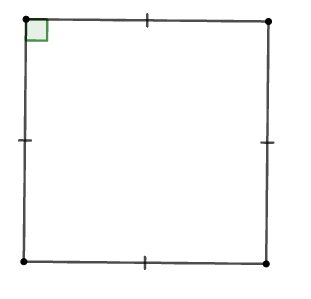
Trong các hình trên, có bao nhiêu đa giác giác đều?
Mỗi góc của bát giác đều nội tiếp đường tròn tâm \[O\] có số đo là