15 câu trắc nghiệm Toán 9 Cánh diều Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn có đáp án
15 câu trắc nghiệm Toán 9 Cánh diều Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn có đáp án
-
37 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho các hình dưới đây:
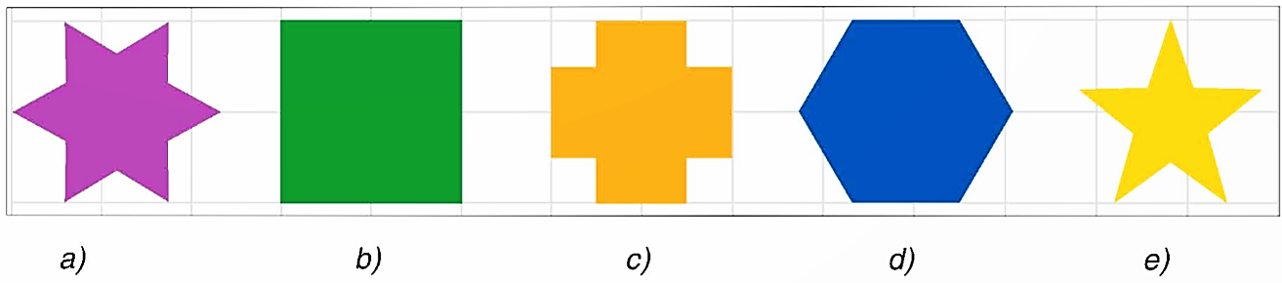
Trong các hình trên, hình nào có dạng là đa giác đều?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Các hình \(a,\,\,c,\,\,e\) không là đa giác đều vì các hình này không phải đa giác lồi.
Hình \[b\] là hình vuông (tứ giác đều), hình \[d\] là lục giác đều.
Câu 2:
Trong các hình phẳng sau, các hình là hình phẳng có dạng là đa giác đều là:
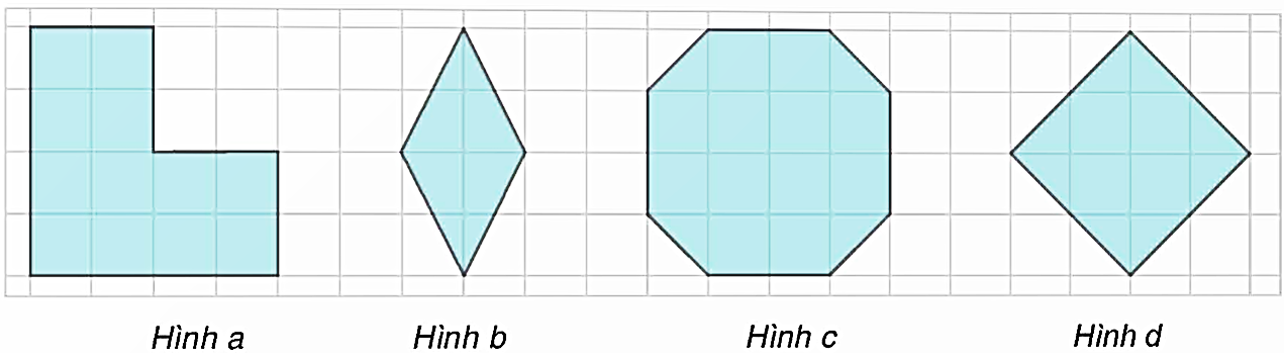
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hình a và c không là đa giác đều vì không có các cạnh bằng nhau.
Hình b không là đa giác đều vì không có các góc bằng nhau.
Hình d là hình vuông (tứ giác đều).
Câu 3:
Đa giác đều là một đa giác
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đa giác đều là một đa giác có các cạnh và các góc bằng nhau.
Câu 4:
Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.
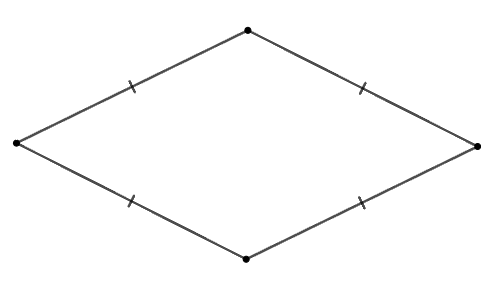
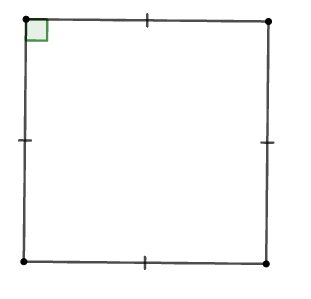
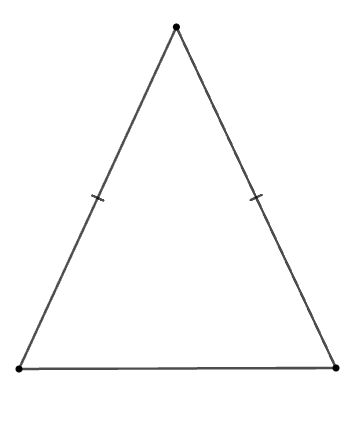
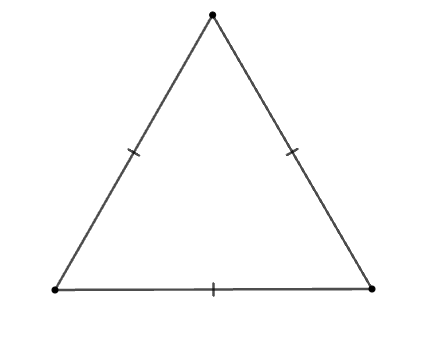
Trong các hình trên, có bao nhiêu đa giác giác đều?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong các hình trên, các đa giác đều là hình vuông (tứ giác đều) và hình tam giác đều.
Vậy có 2 đa giác đều trong các hình trên.
Câu 5:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Lục giác đều là hình lục giác có 6 cạnh và 6 góc bằng nhau.
Hình thoi là đa giác không đều có 4 cạnh bằng nhau và 4 góc không bằng nhau, các góc đối đỉnh của hình thoi bằng nhau.
Ngũ giác có năm cạnh và năm góc bằng nhau là ngũ giác đều.
Hình chữ nhật là đa giác không đều do các cạnh không bằng nhau. Các góc của hình chữ nhật bằng nhau và bằng \(90^\circ \).
Vậy khẳng định sai là B.
Câu 6:
II. Thông hiểu
Số đường tròn nội tiếp của một đa giác đều là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Mỗi đa giác đều có chỉ một đường tròn nội tiếp.
Câu 7:
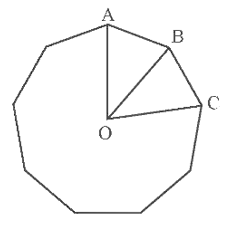
Mỗi góc của bát giác đều nội tiếp đường tròn tâm \[O\] có số đo là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
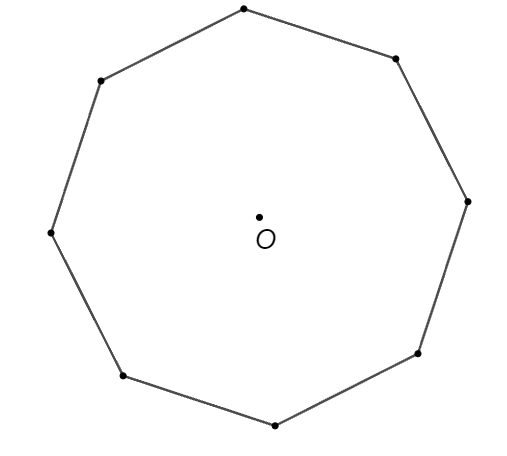
Số đo mỗi góc của một bát giác đều là:
\(\frac{{180^\circ .\left( {8 - 2} \right)}}{8} = 135^\circ \).
Vậy số đo mỗi góc của một bát giác đều là \(135^\circ \).
Câu 8:
Mỗi góc của lục giác đều nội tiếp đường tròn tâm \[O\] có số đo là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
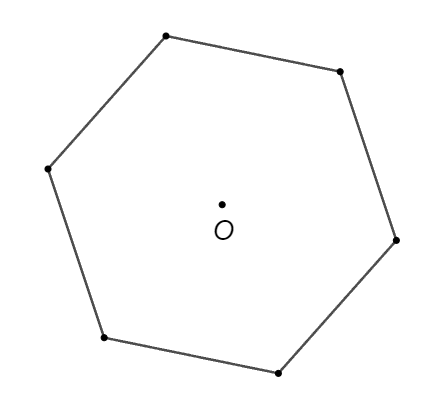
Số đo mỗi góc của một lục giác đều là:
\(\frac{{180^\circ .\left( {6 - 2} \right)}}{6} = 120^\circ \).
Vậy số đo mỗi góc của một lục giác đều là \(120^\circ \).
Câu 9:
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hình vuông có 4 cạnh bằng nhau và 4 góc bằng nhau nên là đa giác đều (tứ giác đều).
Câu 10:
Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là \(5{\rm{ cm}}\). Chu vi đa giác đều này là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Chu vi đa giác đều 11 cạnh đã cho là: \(11.5 = 55{\rm{ }}\left( {{\rm{cm}}} \right)\).
Câu 11:
Cho ngũ giác đều \[ABCDE\]. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
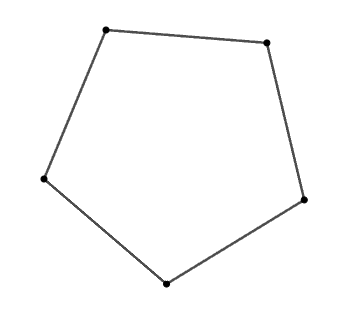
Tổng các góc trong của một ngũ giác đều là:
\(180^\circ \left( {5 - 2} \right) = 540^\circ \).
Câu 12:
Tổng số đo các góc của đa giác đều 7 cạnh là:
 Xem đáp án
Xem đáp án
Đáp án đúng là:
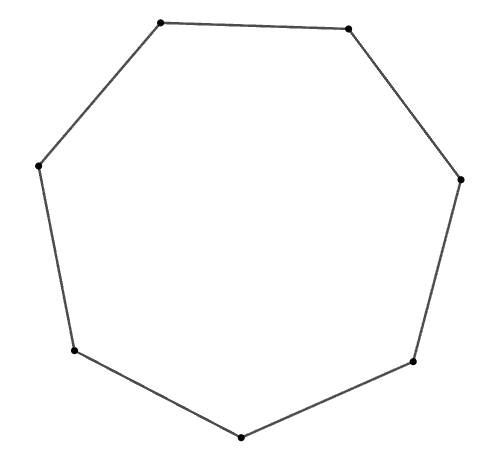
Tổng các góc trong của một đa giác đều 7 cạnh là:
\(180^\circ \left( {7 - 2} \right) = 900^\circ \).
Câu 14:
Số cạnh của đa giác đều có số đường chéo bằng số cạnh là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Giả sử đa giác đều đó có \[n\] cạnh.
Từ mỗi đỉnh của hình \[n\] – giác lồi kẻ được \(n - 1\) đoạn thẳng đến các đỉnh còn lại, trong đó có hai đoạn thẳng là cạnh của đa giác, \(n - 3\) đoạn thẳng là đường chéo.
Đa giác có n đỉnh nên kẻ được \(n\left( {n - 3} \right)\) đường chéo, trong đó mỗi đường chéo tính 2 lần.
Vậy số đường chéo của hình n - giác lồi là \(\frac{{n\left( {n - 3} \right)}}{2}\).
Đa giác đều có số đường chéo bằng số cạnh nên \(\frac{{n\left( {n - 3} \right)}}{2} = n\), suy ra \(n = 5\).
Câu 15:
Một lục giác đều và một ngũ giác đều chung cạnh \[AD\] (như hình vẽ).
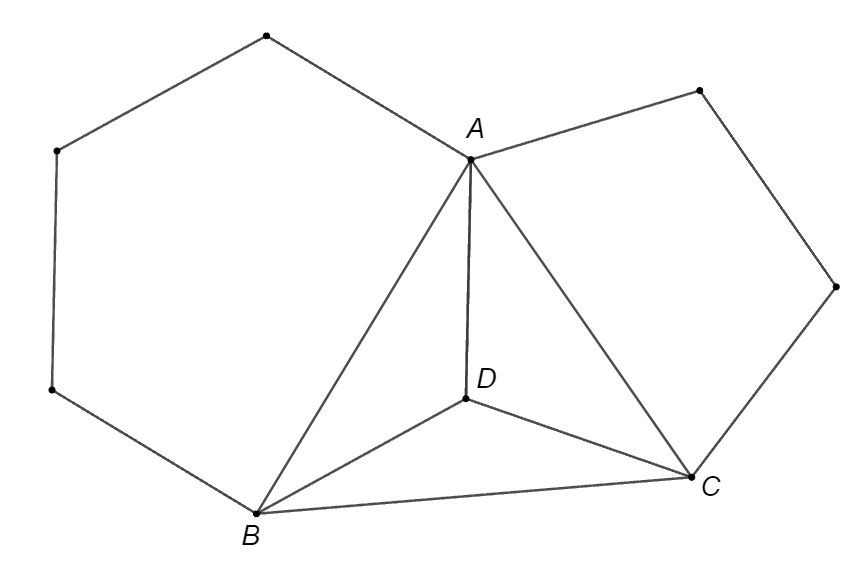
Số đo góc \(BAC\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo công thức tính góc của đa giác đều, ta có:
\(\widehat {ADB} = \frac{{180^\circ \left( {6 - 2} \right)}}{6} = 120^\circ \).
Tam giác \[DBA\] cân tại \[D\] nên \(\widehat {DAB} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Tương tự, ta tính được \(\widehat {DAC} = 36^\circ \).
Vậy \(\widehat {BAC} = \widehat {DAB} + \widehat {DAC} = 30^\circ + 36^\circ = 66^\circ \).