Phần thực của số phức là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án C
Ta có:
Cho m là số thực, biết phương trình có hai nghiệm phức. Tính tổng môđun của hai nghiệm.
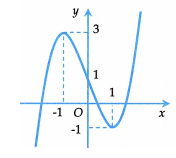
Cho hàm số đa thức bậc ba liên tục trên R và có đồ thị như hình vẽ. Với m là tham số thực bất kì thuộc đoạn , phương trình có bao nhiêu nghiệm thực phân biệt?
Tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện là đường elip . Phương trình đường elip là
Cho các thực dương a và số thực b khác 0. Mệnh đề nào sau đây là đúng?
Cho hình chóp S.ABC có mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu S lên mặt phẳng là điểm H nằm trong tam giác ABC sao cho . Biết tổng diện tích các mặt cầu ngoại tiếp các hình chóp là . Tính thể tích khối chóp S.ABC
Cho mặt nón có góc ở đỉnh bằng , thiết diện qua trục của hình nón là một tam giác cân có bán kính đường tròn ngoại tiếp bằng 1. Tính chiều cao h của hình nón .
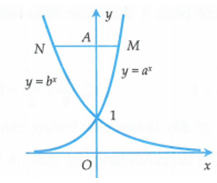
Cho các số thực dương a, b khác 1. Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt đồ thị các hàm số trục tung lần lượt tại M, N, a thì . Mệnh đề nào dưới đây đúng?
Tìm tất cả giá trị của tham số thực m để phương trình có đúng bốn nghiệm phân biệt thuộc đoạn
Cho tứ diện OPQR có OP, OQ, OR đôi một vuông góc. Gọi A, B, C lần lượt là trung điểm các cạnh RQ, PR, PQ. Biết rằng mặt phẳng vuông góc với mặt phẳng , tính giá trị của biểu thức .
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm sao cho khoảng cách từ đến mặt phẳng lớn nhất.
Cho các hàm số , có bao nhiêu hàm số đồng biến trên tập xác định?
Bạn Dũng bắt đầu đi làm ở công ti A với mức lương khởi điểm là 10 triệu đồng một tháng. Cứ sau 2 năm thì lương của bạn Dũng tăng thêm 30%. Hỏi nếu tiếp tục làm ở công ty này sau tròn 11 năm thì tổng tiền lương của bạn Dũng nhận được là bao nhiêu?