Cho hàm số có đồ thị như hình vẽ. Tìm số cực trị của hàm số
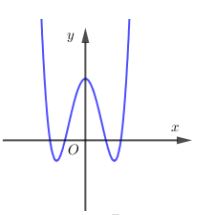
A. 5
B. 6
C. 7
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
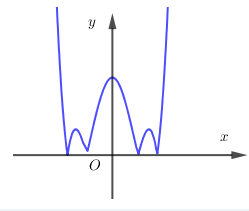
HD: Ta có: Giữ nguyên phần phía trên trục hoành, lấy đối xứng phần phía dưới trục hoành của đồ thị đã cho, ta được đồ thị hàm số Hàm số có 7 cực trị.
Gọi M là giao điểm của đồ thị hàm số với trục Oy. Phương trình tiếp tuyến với đồ thị trên tại điểm M là:
Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
Cho hàm số có đồ thị và đường thẳng . Tìm số các giá trị của m để d cắt tại 3 điểm phân biệt có hoành độ tại thỏa mãn
Hỏi có bao nhiêu giá trị m nguyên trong đoạn để hàm số đồng biến trên khoảng ?
Gọi M, N là các điểm cực tiểu của đồ thị hàm số . Độ dài đoạn thẳng MN bằng:
Thể tích của khối lăng trụ tứ giác đều là Diện tích toàn phần nhỏ nhất của hình lăng trụ là
Cho hàm số đồ thị là và . Gọi h là khoảng cách từ điểm A đến đường thẳng đi qua điểm cực đại, cực tiểu của . Giá trị lớn nhất của h bằng
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
Tìm tất cả các giá trị của để phương trình f(x)=m có 3 nghiệm phân biệt