Cho hình thang cân ABCD có đáy nhỏ AB=1, đáy lớn CD=3, cạnh bên . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng:
A. .
B. .
C. .
D. .
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Ta có:
Khi đó:
Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:
Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:
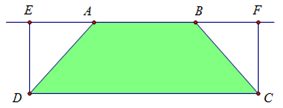
Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a, góc giữa mặt phẳng (A'BC) và mặt phẳng (ABC) bằng . Thể tích khối lăng trụ ABCA'B'C' tính theo a là:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 3a. Thể tích khối chóp S.ABC tính theo a là:
Cho hàm số có đồ thị (C). Nếu (C) có tiệm cận ngang là đường thẳng y=2 và tiệm cận đứng là đường thẳng thì các giá trị của a và b lần lượt là :
Có bao nhiêu số nguyên m để phương trình có hai nghiệm thỏa mãn ?
Cho hình lăng trụ ABC.A'B'C' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng (ABB'A') là tâm của hình bình hành ABB'A'. Thể tích khối lăng trụ ABC.A'B'C' tính theo a là:
Cho hình chóp S.ABC có , Mlà điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng:
Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh của hình nón là: