Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)
- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).
Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.
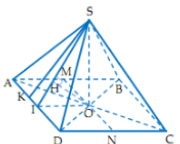
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.
Cho a, b, c là ba số thực dương, khác 1 và . Biết và Khi đó, giá trị của bằng bao nhiêu?
Cho hàm số xác định, liên tục và có đạo hàm trên đoạn Xét các khẳng định sau:
1. Hàm số đồng biến trên thì
2. Giả sử suy ra hàm số nghịch biến trên
3. Giả sử phương trình có nghiệm là khi đó nếu hàm số đồng biến trên thì hàm số nghịch biến trên
4. Nếu , thì hàm số đồng biến trên
Số khẳng định đúng trong các khẳng định trên là
Cho tam giác ABC vuông tại A, AB=a, BC=2a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC.
Cho khối chóp S.ABC có thể tích là . Tam giác SAB có diện tích là . Tính khoảng cách d từ C đến mặt phẳng (SAB).
Cho phương trình:
(với m là tham số). Gọi là tập các giá trị của m để phương trình có nghiệm trên đoạn . Tính a+b.