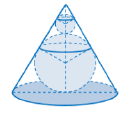
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nó. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Tính bán kính hai khối cầu dựa vào các mối quan hệ đường tròn nội tiếp tam giác.
Tính thể tích hai khối cầu đã cho theo công thức và suy ra kết luận.
Cách giải: Cắt món đồ chơi đó bằng mặt phẳng đứng đi qua trục hình nón.
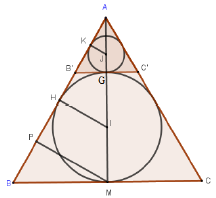
Gọi P, H, K lần lượt là hình chiếu vuông góc của M, I, J trên AB.
Vì
đều.
Vì IM là bán kính mặt cầu nội tiếp tam giác đều ABC nên
Gọi là tiếp tuyến chung của hai đường tròn. Vì đều nên dẫn đến đều.
Suy ra bán kính đường tròn nội tiếp:
Vậy tổng thể tích là:
Chú ý khi giải:
Cần chú ý vận dụng các mối quan hệ đường tròn nội, ngoại tiếp tam giác đều trong việc tính bán kính các khối cầu.
Cho a, b, c là ba số thực dương, khác 1 và . Biết và Khi đó, giá trị của bằng bao nhiêu?
Cho hàm số xác định, liên tục và có đạo hàm trên đoạn Xét các khẳng định sau:
1. Hàm số đồng biến trên thì
2. Giả sử suy ra hàm số nghịch biến trên
3. Giả sử phương trình có nghiệm là khi đó nếu hàm số đồng biến trên thì hàm số nghịch biến trên
4. Nếu , thì hàm số đồng biến trên
Số khẳng định đúng trong các khẳng định trên là
Cho tam giác ABC vuông tại A, AB=a, BC=2a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC.
Cho khối chóp S.ABC có thể tích là . Tam giác SAB có diện tích là . Tính khoảng cách d từ C đến mặt phẳng (SAB).
Cho phương trình:
(với m là tham số). Gọi là tập các giá trị của m để phương trình có nghiệm trên đoạn . Tính a+b.