Cho hình thang cân ABCD (AB // CD); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.
A.
B.
C. 12
D.
 Giải bởi Vietjack
Giải bởi Vietjack
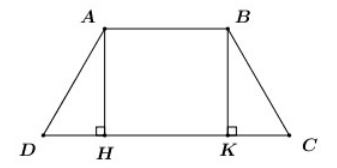
Kẻ AH, BK cùng cuông góc với CD (H, K CD)
Xét tứ giác ABKH có:, suy ra ABKH là hình bình hành.
Lại có nên ABKH là hình chữ nhật, do đó HK = AB = 4
AD = BC (tính chất hình thang cân)
= ACK (tính chất hình thang cân)
(cạnh huyền – góc nhọn)
=> DH = CK (hai cạnh tương ứng)
Mà DH + CK = CD – HK = 8 – 4 = 4
Do đó DH = CK = 2
Áp dụng định lý Py-ta-go trong tam giác vuông ADH ta có:
Vậy diện tích hình thang ABCD là:
Đáp án cần chọn là: B
Cho ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
Cho tam giác ABC có AB = 4cm, AC = , BC = 8cm.Tính số đo , và độ dài đường cao AH của ABC
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 4,5cm
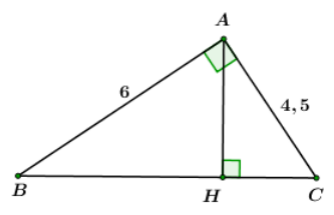
Tính các góc B, C và đường cao AH của tam giác?
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
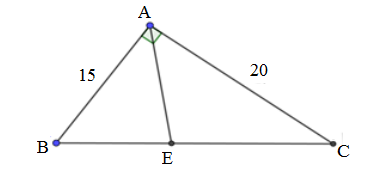
Giải tam giác ABC:
Giải tam giác vuông ABC, biết và BC = 50cm; (làm tròn đến chữ số thập phân thứ nhất).
Cho tam giác ABC vuông tại A có AB = 21cm; , phân giác BD (D thuộc AC). Độ dài phân giác BD là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
Cho tam giác ABC vuông tại A, và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC
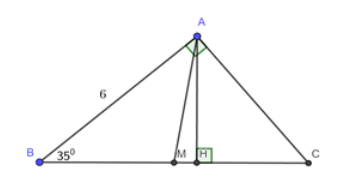
Giải tam giác ABC.
Cho ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH = 3cm; HB = 4cm. Hãy tính AB, AC, AM và diện tích tam giác ABC.
Cho hình thang vuông ABCD có hai đáy AB = 12cm, DC = 16cm, cạnh xiên AD = 8cm. Tính các góc và cạnh góc vuông của hình thang.
Cho MNP vuông tại M có đường cao MH. Gọi I, K lần lượt là hình chiếu vuông góc của H trên MN, MP. Biết HK = 9cm, HI = 6cm. Khi đó tính độ dài các cạnh của MNP.
Cho tứ giác ABCD có AB = AC = AD = 20cm, và . Kẻ BE DC kéo dài.
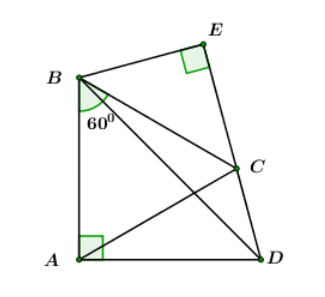
Tính BE?
Cho tam giác ABC vuông tại A, có AC = 14, BC = 17. Khi đó tan B bằng: