Trắc nghiệm Toán 9 Bài Ôn tập chương (có đáp án): Hệ thức lượng trong tam giác vuông (phần 2)
Trắc nghiệm Toán 9 Bài Ôn tập chương (có đáp án): Hệ thức lượng trong tam giác vuông (phần 2)
-
1608 lượt thi
-
34 câu hỏi
-
34 phút
Danh sách câu hỏi
Câu 1:
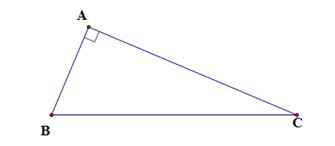
Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
 Xem đáp án
Xem đáp án
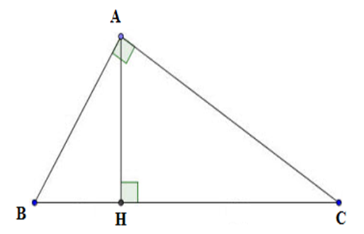
Ta thấy AH. BC = AB. AC nên D sai
Đáp án cần chọn là: D
Câu 2:
Cho hình vẽ sau:
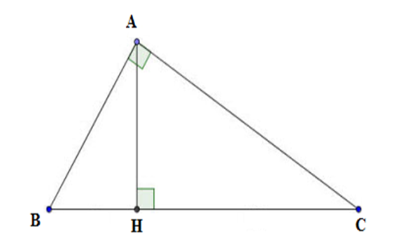
Chọn câu sai.
 Xem đáp án
Xem đáp án
+ Xét tam giác AHB vuông tại H có sin B = nên A đúng.
+ Xét tam giác ABC vuông tại A có cos C = nên B đúng.
+ Xét tam giác ABC vuông tại A có tan B = nên C đúng.
+ Xét tam giác AHC vuông tại H có tan C = nên D sai
Đáp án cần chọn là: D
Câu 3:
Chọn câu đúng nhất. Nếu là một góc nhọn bất kì, ta có:
 Xem đáp án
Xem đáp án
Nếu là một góc nhọn bất khì thì ; ;
nên cả A, B, C đều đúng
Đáp án cần chọn là: D
Câu 4:
Cho là hai góc nhọn bất kì . Chọn câu đúng.
 Xem đáp án
Xem đáp án
Vậy A, B, D sai, C đúng
Đáp án cần chọn là: C
Câu 5:
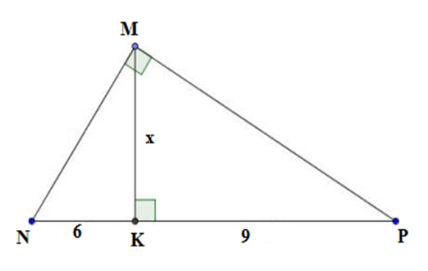
Tính giá trị của x trên hình vẽ:
 Xem đáp án
Xem đáp án
Xét tam giác MNP vuông tại M, có MKNP ta có (hệ thức lượng trong tam giác vuông)
Đáp án cần chọn là: C
Câu 7:
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
 Xem đáp án
Xem đáp án

Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
= BH. BC => BH =
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là: B
Câu 8:
Giải tam giác vuông ABC, biết và BC = 50cm; (làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
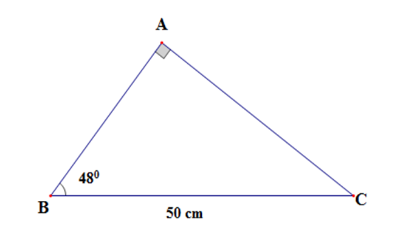
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
Vậy AC = 37,2cm; AB = 33,5cm;
Đáp án cần chọn là: D
Câu 9:
Cho tam giác ABC vuông tại A có AB = 21cm; , phân giác BD (D thuộc AC). Độ dài phân giác BD là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
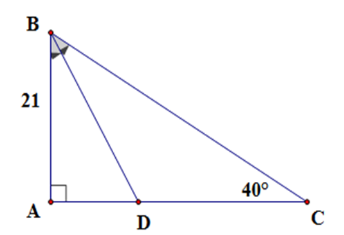
Xét tam giác ABC vuông tại A có
Mà BD là phân giác góc ABC nên
Xét tam giác ABD vuông tại A ta có
Đáp án cần chọn là: D
Câu 10:
Cho tam giác ABC vuông tại A, có AC = 14, BC = 17. Khi đó tan B bằng:
 Xem đáp án
Xem đáp án
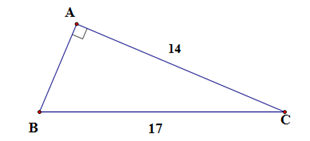
Xét tam giác ABC vuông tại A, theo định lý Py-ta-go ta có:
Đáp án cần chọn là: C
Câu 12:
Cạnh bên của tam giác ABC cân tại A dài 20cm, góc ở đáy là . Độ dài cạnh đáy của tam giác cân là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
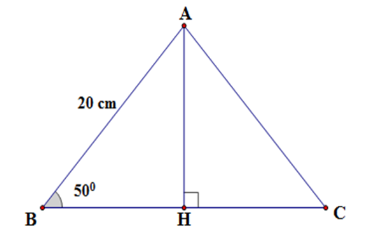
Kẻ AHBC tại H. Suy ra H là trung điểm BC (do tam giác ABC cân tại A có AH vừa là đường cao vừa là đường trung tuyến)
Xét tam giác AHB vuông tại H có:
Mà H là trung điểm của BC nên:
Đáp án cần chọn là: B
Câu 13:
Cho hình vẽ, tìm x.
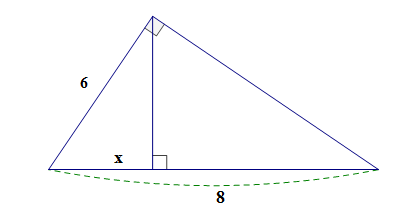
 Xem đáp án
Xem đáp án
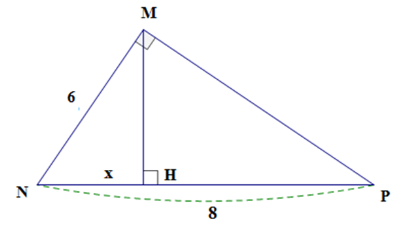
Đặt tên như hình vẽ trên.
Tam giác MNP vuông tại M có MHNP
Theo hệ thức lượng trong tam giác vuông ta có:
Vậy x = 4,5
Đáp án cần chọn là: B
Câu 14:
Cho . Giá trị biểu thức:
 Xem đáp án
Xem đáp án
Vì nên . Chia cả từ và mẫu của M cho cos ta được:
Thay vào M ta được:
Đáp án cần chọn là: A
Câu 15:
Tìm x; y trong hình vẽ sau:
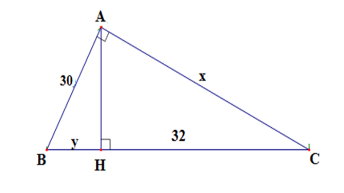
 Xem đáp án
Xem đáp án
Ta có: BC = BH + HC = y + 32
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
Suy ra y = 18 => BC = 18 + 32 = 50
Áp dụng hệ thức lượng ta có:
Vậy c = 40; y = 18
Đáp án cần chọn là: D
Câu 16:
Tính số đo góc nhọn x, biết
 Xem đáp án
Xem đáp án
=> cos x = (do x là góc nhọn nên cos x > 0)
Suy ra
Đáp án cần chọn là: B
Câu 17:
Cho ABC vuông tại A. Biết . Đường cao AH = 15cm. Tính HC.
 Xem đáp án
Xem đáp án
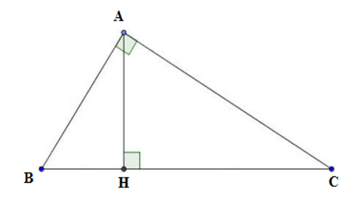
Vì => AB = 5a; AC = 7a với a > 0
Theo hệ thức lượng trong tam giác ABC vuông tại A ta có:
Suy ra AB = ; AC =
Lại có AH. BC = AB.AC
Đáp án cần chọn là: D
Câu 18:
Cho ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
 Xem đáp án
Xem đáp án
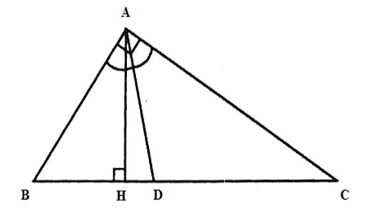
Xét tam giác vuông ABC ta có:
Vì AD là phân giác góc A nên theo tính chất đường phân giác trong tam giác ta có:
Suy ra BD = 12. = cm
Theo hệ thức lượng trong tam giác vuông ABC ta có:
Đáp án cần chọn là: A
Câu 20:
Cho biết . Tính giá trị biểu thức:
 Xem đáp án
Xem đáp án
Vì nên .
Chia cả từ và mẫu của M cho ta được:
Thay ta được:
Đáp án cần chọn là: D
Câu 23:
Cho đoạn thẳng AB = 2a và trung điểm O của nó. Trên nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Qua O vẽ một tia cắt Ax tại M sao cho . Qua O vẽ tia thứ hai cắt By tại N sao cho . Khi đó, diện tích tam giác MON là:
 Xem đáp án
Xem đáp án
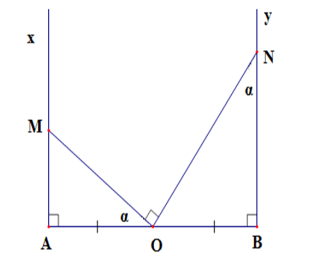
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
Vậy diện tích tam giác MON là:
Đáp án cần chọn là: A
Câu 24:
Cho hình thang cân ABCD (AB // CD); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.
 Xem đáp án
Xem đáp án
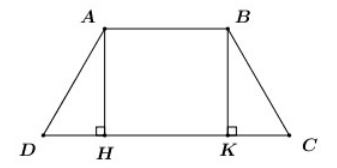
Kẻ AH, BK cùng cuông góc với CD (H, K CD)
Xét tứ giác ABKH có:, suy ra ABKH là hình bình hành.
Lại có nên ABKH là hình chữ nhật, do đó HK = AB = 4
AD = BC (tính chất hình thang cân)
= ACK (tính chất hình thang cân)
(cạnh huyền – góc nhọn)
=> DH = CK (hai cạnh tương ứng)
Mà DH + CK = CD – HK = 8 – 4 = 4
Do đó DH = CK = 2
Áp dụng định lý Py-ta-go trong tam giác vuông ADH ta có:
Vậy diện tích hình thang ABCD là:
Đáp án cần chọn là: B
Câu 25:
Cho hình thang vuông ABCD có hai đáy AB = 12cm, DC = 16cm, cạnh xiên AD = 8cm. Tính các góc và cạnh góc vuông của hình thang.
 Xem đáp án
Xem đáp án
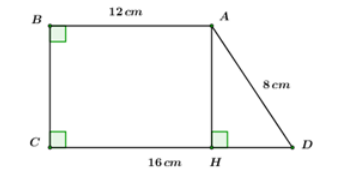
Có hình thang vuông ABCD cạnh xiên AD
Dễ thấy ABCH là hình chữ nhật (có 3 góc vuông) => HC = AB = 12cm
HD = DC – HC = 16 – 12 = 4 (cm)
Áp dụng định lý Pytago cho AHD vuông tại H ta có:
Xét AHD vuông tại H ta có:
Đáp án cần chọn là: B
Câu 26:
Cho tứ giác ABCD có AB = AC = AD = 20cm, và . Kẻ BE DC kéo dài.
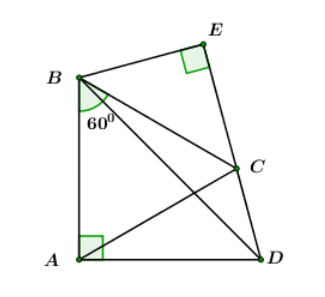
Tính BE?
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago cho ABD vuông tại A ta có:
Theo đề bài ta có:
Lại có: AC = AD = 20cm => ACD cân tại A
Xét BED vuông tại E ta có:
Đáp án cần chọn là: A
Câu 27:
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là , chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.
 Xem đáp án
Xem đáp án
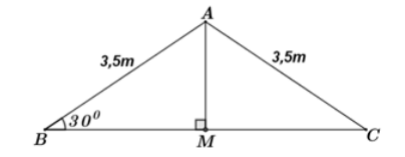
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: ABC cân tại A
Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.
Gọi M là trung điểm của BC.
=> AM là đường trung tuyến đồng thời là đường cao của ABC (tính chất).
Xét ABM vuông tại M ta có:
Vậy bề rộng mái nhà là 6,06m
Đáp án cần chọn là: B
Câu 28:
Cho tam giác ABC có diện tích là . Điểm D ở giữa BC sao cho BC = 5DC, điểm E ở giữa AC sao cho AC = 4AE, hai điểm F, G ở giữa BE sao cho BE = 6GF = 6GE. Tính diện tích tam giác DGF.
 Xem đáp án
Xem đáp án
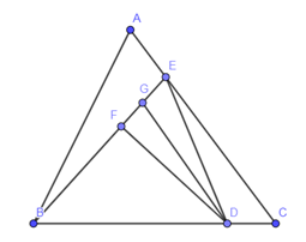
Ta kí hiệu d(A; BC) là khoảng cách từ A đến đường thẳng BC (nghĩa là độ dài đoạn vuông góc kẻ từ A đến BC), tương tự với những kí hiệu khác trong bài.
Ta có:
Đáp án cần chọn là: B
Câu 29:
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
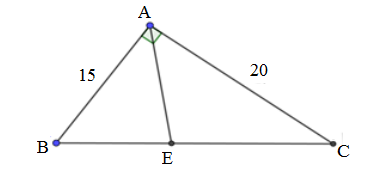
Giải tam giác ABC:
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago cho vuông tại A có:
Đáp án cần chọn là: B
Câu 30:
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 4,5cm
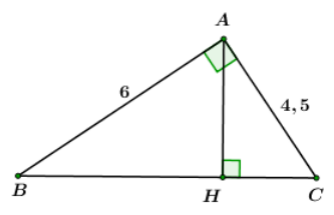
Tính các góc B, C và đường cao AH của tam giác?
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago cho ABC vuông tại A, có:
Xét ABC vuông tại A ta có:
sin B = B 36o52’
Vì vuông tại A ta có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH. 7,5 = 4,5. 6 => AH = 3,6
Đáp án cần chọn là: B
Câu 31:
Cho tam giác ABC vuông tại A, và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC
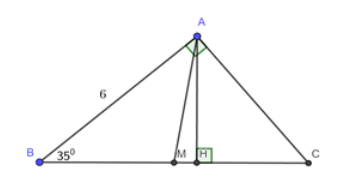
Giải tam giác ABC.
 Xem đáp án
Xem đáp án
Xét ABC vuông tại A ta có:
Vì ABC vuông tại A ta có:
Đáp án cần chọn là: C
Câu 32:
Cho ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH = 3cm; HB = 4cm. Hãy tính AB, AC, AM và diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
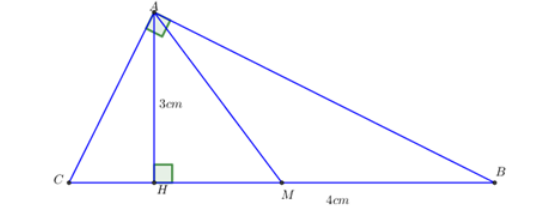
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
+) Áp dụng hệ thức về cạnh và đường cao trng tam giác vuông ABC với AH là đường cao ta có:
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có:
+) Diện tích tam giác ABC với AH là đường cao ta có:
Vậy AB = 5cm, AC = cm; AM = cm; .
Đáp án cần chọn là: A
Câu 33:
Cho tam giác ABC có AB = 4cm, AC = , BC = 8cm.Tính số đo , và độ dài đường cao AH của ABC
 Xem đáp án
Xem đáp án
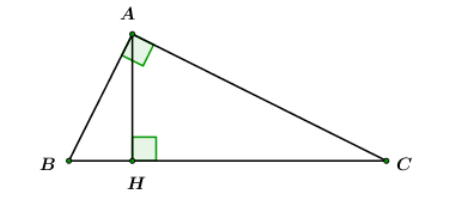
+) Chứng minh tam giác ABC vuông
Ta có:
+) Tính số đo B, C và độ dài đường cao AH của ABC
Áp dụng tỉ số lượng giác của góc nhọn trong ABC và có đường cao AH ta có:
Đáp án cần chọn là: D
Câu 34:
Cho MNP vuông tại M có đường cao MH. Gọi I, K lần lượt là hình chiếu vuông góc của H trên MN, MP. Biết HK = 9cm, HI = 6cm. Khi đó tính độ dài các cạnh của MNP.
 Xem đáp án
Xem đáp án
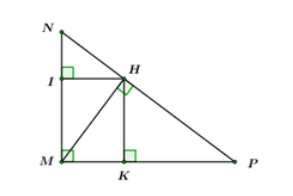
Xét tứ giác MIHK ta có
=> MIHK là hình chữ nhật (dhnb)
=> HI = ML = 6cm
Áp dụng định lý Pytago cho MHK vuông tại K ta có:
Áp dụng hệ thức lượng trong MHP vuông tại H có đường cao HI ta có:
Áp dụng định lý Pytago cho MNP vuông tại N ta có:
Đáp án cần chọn là: B