Cho hàm số bậc 4 có đồ thị như hình vẽ.
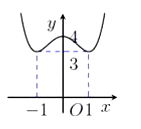
Có bao nhiêu giá trị nguyên của tham số m và để phương trình có hai nghiệm dương phân biệt?
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
Từ đồ thị hàm số, ta có y = f(x) có 3 điểm cực trị là -1, 0, 1 nên hàm số có dạng
và đồ thị hàm số f(x) đi qua hai điểm nên
Điều kiện suy ra m > 0.
Ta có
do x + 1 > 0 (*)
Xét hàm số với t > 0. Ta có
Từ (*) ta có
Đặt khi đó
Dễ thấy với mỗi giá trị của u cho ta hai giá trị của x > 0 nên yêu cầu bài toán đưa về điều kiện là tìm m để phương trình có đúng một nghiệm Đặt với
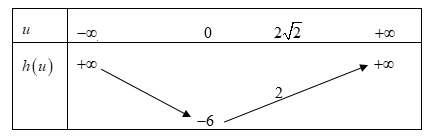
Do nên có 2019 giá trị thỏa mãn.
Biết tập hợp các điểm biểu diễn số phức trong mặt phẳng tọa độ Oxy là một đường thẳng. Khi đó mô đun của z bằng
Trong không gian Oxyz, cho . Gọi P là mặt phẳng chứa cạnh BC và vuông góc với (ABC). (C) là đường tròn đường kính BC nằm trong mặt phẳng (P). Gọi S là một điểm bất kì nằm trên (C) khác B, C. Khi đó khoảng cách từ tâm mặt cầu ngoại tiếp tứ diện S.ABC đến mặt phẳng là
Trên mặt phẳng (Oxy) biết M(-2; 1) là điểm biểu diễn số phức z. Môđun của z bằng
Cho hàm số f(x) có tập xác định và có bảng xét dấu f'(x) như sau:

Số điểm cực tiểu của hàm số đã cho là
Cho phương trình (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của để phương trình đã cho có nghiệm?
Cho hình trụ có bán kính đáy r = 3 và độ dài đường sinh l = 3. Diện tích xung quanh của hình trụ đã cho bằng
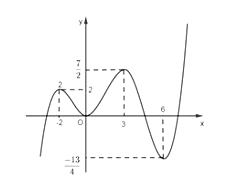
Cho hàm số y = f(x) có bảng biến thiên như sau
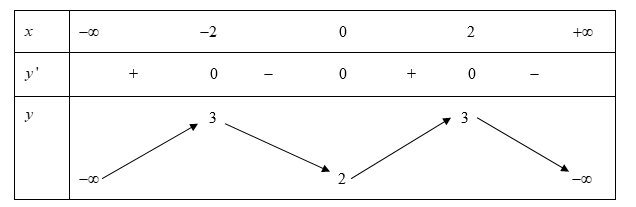
Số điểm cực trị của hàm số đã cho là
Trong không gian Oxyz cho ba điểm Mặt phẳng (ABC) có phương trình là