Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng \(a.\) Gọi \(M;N\) lần lượt là trung điểm của \(SA\) và \(BC.\) Biết góc giữa \(MN\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^0}.\) Khoảng cách giữa hai đường thẳng \(BC\) và \(DM\) là:
A.\(a\sqrt {\frac{{15}}{{17}}} \)
B.\(a\sqrt {\frac{{15}}{{62}}} \)
C.\(a\sqrt {\frac{{30}}{{31}}} \)
D. \(a\sqrt {\frac{{15}}{{68}}} \)
 Giải bởi Vietjack
Giải bởi Vietjack
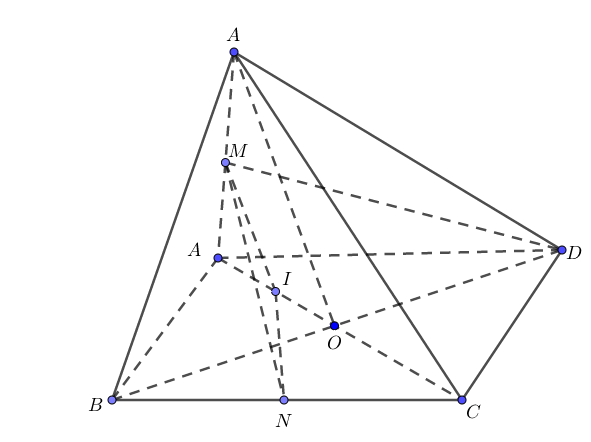
Gọi \(O\) là tâm của đáy \(ABCD\) ta có \(SO \bot \left( {ABCD} \right)\)
Gọi \(I\) là trung điểm của OA
\( \Rightarrow MI//SO \Rightarrow MI \bot \left( {ABCD} \right) \Rightarrow \left( {MN,\left( {ABCD} \right)} \right) = \angle \left( {MN,\left( {ABCD} \right)} \right) = \angle MNI = {60^0}\)
Xét \(\Delta NCI\) có \(CN = \frac{1}{2}BC = \frac{a}{2};CI = \frac{3}{4}AC = \frac{{3\sqrt 2 }}{4}a;\angle NCI = {45^0}\)
Suy ra \(NI = \sqrt {C{N^2} + C{I^2} - 2CN.CI.\cos C} = \sqrt {\frac{{{a^2}}}{4} + \frac{{18{a^2}}}{{16}} - 2.\frac{a}{2}.\frac{{3\sqrt 2 }}{4}.a.\cos {{45}^0}} = a\frac{{\sqrt {10} }}{4}.\)
\(MI = NI.\tan {60^0} = a\frac{{\sqrt {30} }}{4} \Rightarrow SO = a\frac{{\sqrt {30} }}{2}.\)
Vì \(\left\{ \begin{array}{l}BC//\left( {SAD} \right)\\DM \subset \left( {SAD} \right)\end{array} \right. \Rightarrow d\left( {BC,DM} \right) = d\left( {BC,\left( {SAD} \right)} \right) = 2d\left( {O,\left( {SAD} \right)} \right) = 2h.\)
Xét tứ diện \(\left( {SAOD} \right)\) có \(SO;OA;OD\) đôi một vuông góc
Nên ta có: \(\frac{1}{{{h^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{2}{{15{a^2}}} + \frac{2}{{{a^2}}} + \frac{2}{{{a^2}}} = \frac{{62}}{{15{a^2}}} \Rightarrow h = a\sqrt {\frac{{15}}{{62}}} \)
Do đó \(d\left( {BC,DM} \right) = 2h = 2a\sqrt {\frac{{15}}{{62}}} = a\sqrt {\frac{{30}}{{31}}} \)
Đáp án C.
Cho hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) khi cạnh đáy của hình chóp giảm đi 3 lần và vẫn giữ nguyên chiều cao thì thể tích của khối chóp giảm đi mấy lần:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Trong đoạn \(\left[ { - 20;20} \right]\), có bao nhiêu số nguyên \(m\) để hàm số \(y = \left| {10f\left( {x - m} \right) - \frac{{ (ảnh 1)](https://video.vietjack.com/upload2/images/1649521444/1649521622-image30.png)
Trong đoạn \(\left[ { - 20;20} \right]\), có bao nhiêu số nguyên \(m\) để hàm số \(y = \left| {10f\left( {x - m} \right) - \frac{{11}}{3}{m^2} + \frac{{37}}{3}m} \right|\) có 3 điểm cực trị?
Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
Thể tích của khối chóp có diện tích đáy bằng B, chiều cao bằng h là:
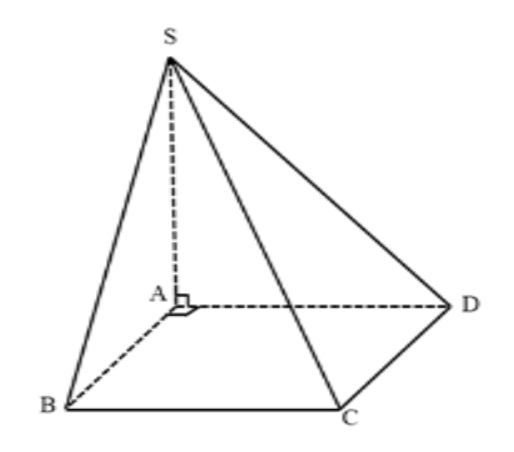
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,AD = a\sqrt 2 ,\) đường thẳng \(SA\) vuông góc với \(mp\left( {ABCD} \right).\) Góc giữa \(SC\) và \(mp\left( {ABCD} \right)\) bằng \({60^0}.\) Tính thể tích khối chóp \(S.ABCD\)
Cho hàm số \(y = \left| {x + \sqrt {16 - {x^2}} } \right| + a\) có giá trị lớn nhất và nhỏ nhất lần lượt là \(m,M,\) Biết \(m + M = {a^2}.\) Tìm tích \(P\) tất cả giá trị \(a\) thỏa mãn đề bài.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên dưới.
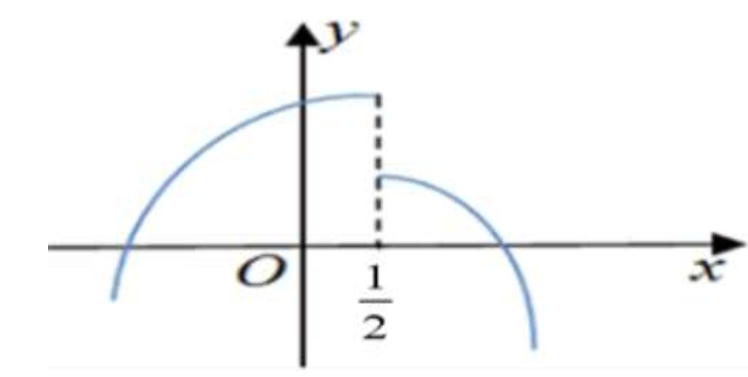
Khi đó
Cho hàm số \(y = \frac{{mx - 8}}{{2x - m}}.\) Tìm tất cả các giá trị thực của tham số \(m\) để hàm số đồng biến trên từng khoảng xác định
Cho tứ diện đều \(ABCD\) có cạnh bằng 1, gọi \(M\) là trung điểm \(AD\) và \(N\) trên cạnh \(BC\) sao cho \(BN = 2NC.\) Khoảng cách giữa hai đường thẳng \(MN\) và \(CD\) là
Một vật có phương trình chuyển động \(S\left( t \right) = 4,9{t^2};\) trong đó t tính bằng (s), S(t) tính bắng mét (m). Vận tốc của vật tại thời điểm t=6s bằng
Giá trị lớn nhất của hàm số \(y = 2{x^3} - 3{x^2} + {10^{2020}}\) trên đoạn \(\left[ { - 1;1} \right]\) là:
Cho hình chóp tứ giác đều \(S.ABCD\) có \(SA = AB = a.\) Góc giữa \(SA\) và \(CD\) là
Đồ thị hàm số \(y = \frac{{x - 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng