Cho mặt cầu \(S\left( {I;R} \right)\) và điểm \(A\) nằm ngoài mặt cầu. Qua \(A\) kẻ đường thẳng cắt \(\left( S \right)\) tại hai điểm phân biệt \(B,C.\) Tích \(AB.AC\) bằng
A.\(I{A^2} - {R^2}.\)
B.\(R.IA.\)
C.\(I{A^2} + {R^2}.\)
D. \(2R.IA.\)
 Giải bởi Vietjack
Giải bởi Vietjack
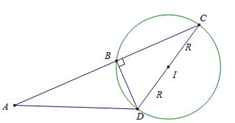
+ Gọi \(D\) là điểm đối xứng của \(C\) qua \(I.\) ta suy ra \(BD \bot AC\)
+ Ta có
\(AB.AC = \overrightarrow {AB} .\overrightarrow {AC} = \left( {\overrightarrow {AD} + \overrightarrow {DB} } \right)\overrightarrow {AC} = \overrightarrow {AD} .\overrightarrow {AC} = \left( {\overrightarrow {AI} + \overrightarrow {ID} } \right)\left( {\overrightarrow {AI} + \overrightarrow {IC} } \right)\)
\( = \left( {\overrightarrow {AI} - \overrightarrow {IC} } \right)\left( {\overrightarrow {AI} + \overrightarrow {IC} } \right) = A{I^2} - I{C^2} = A{I^2} - {R^2}.\)
Đáp án A
Với giá trị nào của \(m\) thì đồ thị hàm số \(y = \frac{{2{x^2} + 6mx + 4}}{{mx + 2}}\) đi qua điểm \(A\left( { - 1;4} \right)?\)
Tìm tất cả các giá trị của tham số \(m\) sao cho đồ thị hàm số \(y = \frac{{\sqrt {x - 1} + 2021}}{{\sqrt {{x^2} - 2mx + m + 2} }}\) có đúng ba đường tiệm cận.
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = m{x^4} + \left( {m - 3} \right){x^2} + 3m - 5\) chỉ có cực tiểu mà không có cực đại.
Số giao điểm của hai đồ thị \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng số nghiệm phân biệt của phương trình nào sau đây?
Tìm \(m\) để phương trình \({x^6} + 6{x^4} - {m^2}{x^3} + \left( {15 - 3{m^2}} \right){x^2} - 6mx + 10 = 0\) có đúng hai nghiệm phân biệt thuộc \[\left[ {\frac{1}{2};2} \right]?\]
Cho đường cong \(\left( C \right)\) có phương trình \(y = \frac{{x - 1}}{{x + 1}}.\) Gọi \(M\) là giao điểm của \(\left( C \right)\) với trục tung. Tiếp tuyến của \(\left( C \right)\) tại \(M\) có phương trình là
Giả sử các biểu thức chứa logarit đều có nghĩa. Mệnh đề nào sau đây đúng?
Cho tứ diện \(ABCD\) có \(AB = 2a,AC = 3a,AD = 4a,\widehat {BAC} = \widehat {CAD} = \widehat {DAB} = {60^0}.\) Thể tích khối tứ diện \(ABCD\) bằng
Cho \(a\) là số thực dương và \(m,n\) là các số thực tùy ý. Trong các tính chất sau, tính chất nào đúng?
Cho đồ thị \(\left( {{C_m}} \right):y = {x^3} - 2{x^2} + \left( {1 - m} \right)x + m.\) Khi thì \(\left( {{C_m}} \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 4.\) Khẳng định nào sau đây đúng?
Đồ thị của hai hàm số \(y = 4{x^4} - 2{x^2} + 1\) và \(y = {x^2} + x + 1\) có tất cả bao nhiêu điểm chung?
Công thức tính thể tích khối chóp có diện tích đáy \(B\) và chiều cao \(h\) là
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B,SA\) vuông góc với đáy và \(SA = AB = 6a.\) Tính thể tích khối chóp \(S.ABC\).