Cho hàm số liên tục trên và thỏa mãn . Khi đó bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Với (*)
Tính
Đặt .
Đổi cận: ; .
Khi đó .
Từ (*), ta được: .
Cho tập hợp gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên một tập con có 3 phần tử của tập hợp S. Tính xác suất để tập hợp được chọn có tổng các phần tử chia hết cho 3.
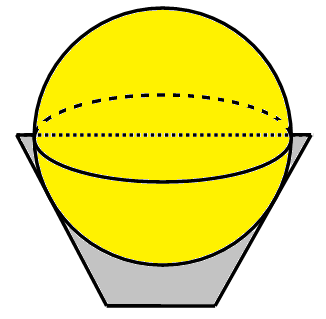
Một cái thùng đựng đầy nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng ba lần bán kính mặt đáy của thùng.Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của thùng nước và đo được thể tích nước tràn ra ngoài là (dm3). Biết rằng khối cầu tiếp xúc với mặt trong của thùng và đúng một nửa của khối cầu đã chìm trong nước (hình vẽ). Thể tích nước còn lại trong thùng có giá trị nào sau đây
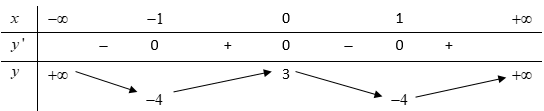
Cho hàm số , liên tục trên và có bảng biến thiên như hình vẽ bên. Tìm số nghiệm thực của phương trình
Trong không gian Oxyz cho điểm và . Phương trình mặt cầu tâm I và đi qua A có phương trình là:
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng (Oxy) biểu diễn các số phức z và. Tính biết diện tích tam giác OAB bằng 8
Trong không gian với hệ tọa độ , cho tứ diện có tọa độ các điểm , , , . Trên các cạnh , , lần lượt lấy các điểm sao cho và tứ diện có thể tích nhỏ nhất. Phương trình mặt phẳng có dạng là . Tính
Một vật chuyển động với gia tốc . Vận tốc của vật tại thời điểm giây là 17 m / s. Quãng đường vật đó đi được trong khoảng thời gian từ thời điểm giây đến thời điểm giây là:
Hàm số và có đồ thị như hình vẽ dưới đây.
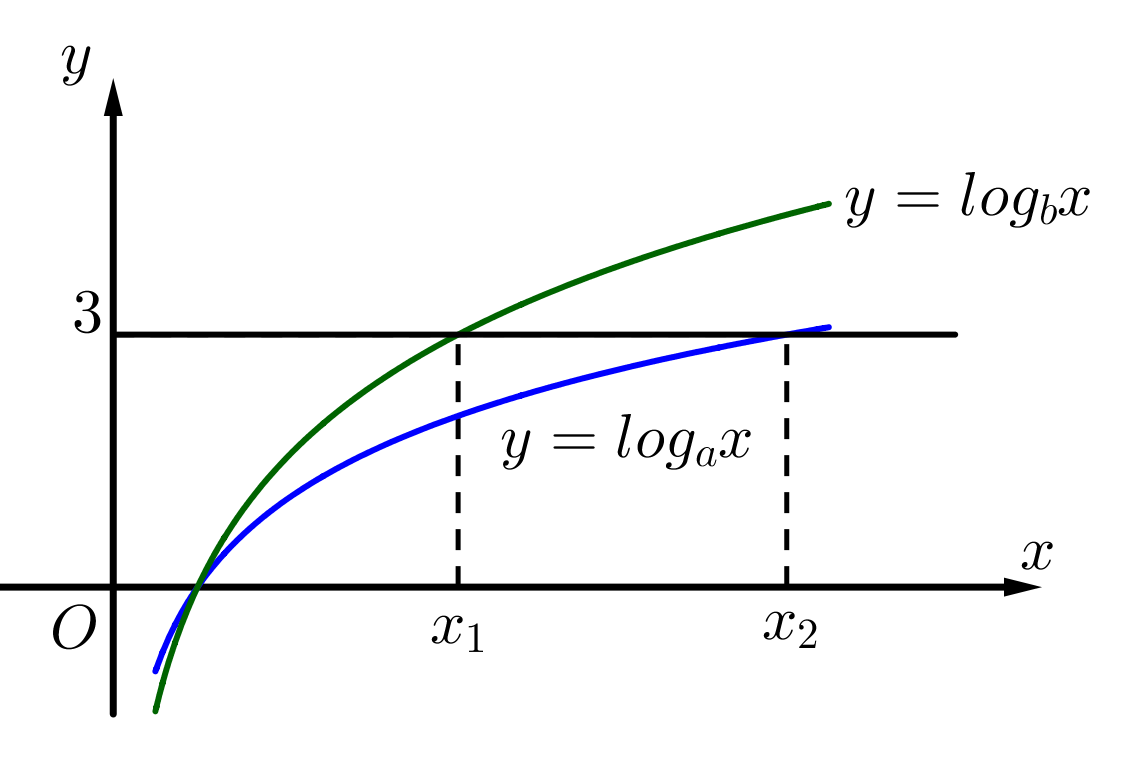
Đường thẳng cắt hai đồ thị tại các điểm có hoành độ , . Biết rằng , giá trị của bằng
Cho hình vuông cạnh trên đường thẳng vuông góc với mặt phẳng tại ta lấy điểm di động không trùng với . Hình chiếu vuông góc của lên lần lượt là . Tìm giá trị lớn nhất của thể tích khối tứ diện .
Cho bất phương trình . Tìm tất cả các giá trị của tham số để bất phương trình có nghiệm đúng