Parabol (P) có phương trình y= -x2 đi qua A và B có hoành độ lần lượt là và .Cho O là gốc tọa độ. Khi đó:
A. Tam giác AOB là tam giác nhọn
B. Tam giác AOB là tam giác đều.
C. Tam giác AOB là tam giác vuông.
D. Tam giác AOB là tam giác có một
 Giải bởi Vietjack
Giải bởi Vietjack
+ Parabol (P) đi qua A, B có hoành độ
là hai điểm đối xứng nhau qua Oy.
Vậy tam giác AOB cân tại O.
+ Gọi I là giao điểm của AB và Oy suy ra ∆ IOA vuông tại I nên:
Vậy ∆AOB là tam giác đều.
Chọn B.
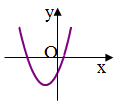
Nếu hàm số y= ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là:
Giá trị nào của m thì đồ thị hàm số y= x2+ 3x+m cắt trục hoành tại hai điểm phân biệt?
Cho parabol (P) ; y= ax2+bx+ c biết: (P) đi qua A(2;3) có đỉnh I( 1;2) . Hỏi a+ b+c bằng bao nhiêu.
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
Xác định parabol (P) ; y= ax2+bx+ c biết (P) đi qua M(4;3) cắt Ox tại N(3;0) và P sao cho ∆ INP có diện tích bằng 1 biết hoành độ điểm P nhỏ hơn 3.
Đỉnh của parabol y =x2+x+m nằm trên đường thẳng y= 3/4 nếu m bằng:
Cho hàm số y=f(x) = ax2+ bx+c. Biểu thức f(x+ 3) -3f( x+ 2) +3f( x+ 1) có giá trị bằng.
Parabol (P) y= m2x2 và đường thẳng (d) y= -4x-1 cắt nhau tại hai điểm phân biệt ứng với:
Cho hàm số y= -3x2-2x+5. Đồ thị hàm số này có thể được suy ra từ đồ thị hàm số y= -3x2 bằng cách
Cho đường thẳng d:(9m2-4) x+(n2-9) y=(n-3 )(3m+2). Với giá trị nào của m và n thì phương trình đã cho là đường thẳng song song với trục Ox?
Cho đồ thị: Tìm giá trị lớn nhất và nhỏ nhất của hàm số với -3≤ x≤ 4