Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) cạnh \[a.\] Biết \(SA = SB = SC = a.\) Đặt \(SD = x\left( {0 < x < a\sqrt 3 } \right).\) Tính \(x\) theo \(a\) sao cho \(AC.SD\) đạt giá trị lớn nhất.
A.\(\frac{{a\sqrt 6 }}{{12}}.\)
B. \(\frac{{a\sqrt 3 }}{2}.\)
C.\(\frac{{a\sqrt 6 }}{2}.\)
D. \(a\sqrt 3 .\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
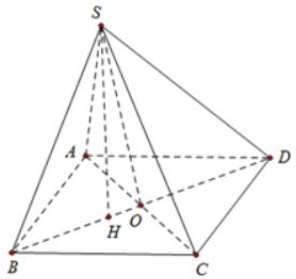
Ta có \(\Delta SAC = \Delta ABC\left( {c - c - c} \right)\) và \(\Delta SAC,\Delta ABC\) lần lượt cân tại \(S\) và \(B.\)
Khi đó \(SO = BO = \frac{{BD}}{2}.\) Suy ra \(\Delta SBD\) vuông tại \(S\) (đường trung tuyến bằng \(\frac{1}{2}\) cạnh đối diện).
Trong \(\Delta SBD\) ta có: \(BD = \sqrt {S{B^2} + S{D^2}} = \sqrt {{a^2} + {x^2}} .\)
Trong \(\Delta ABD\) áp dụng công thức đường trung tuyến ta có:
\(AO = \sqrt {\frac{{2\left( {A{B^2} + A{D^2}} \right)}}{4} - \frac{{B{D^2}}}{4}} = \sqrt {\frac{{2\left( {{a^2} + {a^2}} \right) - \left( {{a^2} + {x^2}} \right)}}{4}} = \frac{{\sqrt {3{a^2} - {x^2}} }}{2}.\)
Suy ra \(AC = 2AO = \sqrt {3{a^2} - {x^2}} .\)
Khi đó \(AC.SD = \sqrt {3{a^2} - {x^2}} .x = \sqrt {\left( {3{a^2} - {x^2}} \right){x^2}} .\)
Áp dụng bất đẳng thức Cauchy (AM-GM) ta có: \(AC.SD = \sqrt {\left( {3{a^2} - {x^2}} \right){x^2}} \le \frac{{3{a^2} - {x^2} + {x^2}}}{2} = \frac{{3{a^2}}}{2}\)
Vậy \(\max AC.SD = \frac{{3{a^2}}}{2}.\)
Dấu “=” xảy ra \(3{a^2} - {x^2} = {x^2} \Leftrightarrow {x^2} = \frac{{3{a^2}}}{2} \Rightarrow x = \frac{{a\sqrt 6 }}{2}.\)
Cho \(x,y,z\) là ba số dương lập thành cấp số nhân; còn \({\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z\) lập thành cấp số cộng. Tính giá trị của biểu thức \(Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x}.\)
Phương trình tiệm cận ngang của đồ thị hàm số \(y = \frac{{4 - 3x}}{{4x + 5}}\) là
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 2x + 3\) tại điểm \(M\left( {2;7} \right)\) là
Mặt cầu \(\left( S \right)\) có tâm \(I\) bán kính \(R\) có diện tích bằng
Cho hàm số \(f\left( x \right) = {x^5} + 3{x^3} - 4m.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f\left( x \right) + m}}} \right) = {x^3} - m\) có nghiệm thuộc đoạn \(\left[ {1;2} \right]?\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,SA\) vuông góc với mặt đáy và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
Đội văn nghệ của lớp 12A có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn ra 2 học sinh của đội văn nghệ sao cho 2 học sinh có 1 học sinh nam và 1 học sinh nữ.
Cho hàm số \(y = - {x^3} - 3\left( {m + 1} \right){x^2} + 3\left( {2m - 1} \right)x + 2020.\) Có bao nhiêu giá trị nguyên \(m\) để hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)?\)
Gọi \(S\) là tập hợp các số tự nhiên có bốn chữ số đôi một khác nhau lập từ các số \(0;1;2;3;4;5;6;7.\) Chọn ngẫu nhiên 1 số từ tập hợp \(S.\) Tính xác suất để số được chọn có đúng 2 chữ số chẵn.
Gọi S là tổng các nghiệm của phương trình \(\log _{\frac{1}{2}}^2x - 6{\log _6}\left( {4x} \right) + 1 = 0.\). Tính giá trị của \(S.\)
Cho \(\left( {{u_n}} \right)\) là một cấp số cộng có \({u_1} = 3\) và công sai d=2. Tìm \({u_{20}}?\)
Số đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} - x}}\) là
Hệ số của \({x^5}\) trong khai triển \({x^2}{\left( {x - 2} \right)^5} + {\left( {2x - 1} \right)^6}\) bằng
Cho hàm số \(f\left( x \right),\) bảng xét dấu của \(f'\left( x \right)\) như sau:

Hàm số \(y = f\left( {1 - 2x} \right)\) nghịch biến trên khoảng nào dưới đây?