Cho đường tròn \(\left( {O;R} \right)\) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA lấy điểm S; SC cắt \(\left( {O;R} \right)\) tại điểm thứ hai là M.
1) Chứng minh \(\Delta SMA\) đồng dạng với \(\Delta SBC\).
2) Gọi H là giao điểm của MAvà BC; K là giao điểm của MD và AB. Chứng minh BMHK là tứ giác nội tiếp và \(HK//CD\).
3) Chứng minh: \(OK.OS = {R^2}\).
 Giải bởi Vietjack
Giải bởi Vietjack
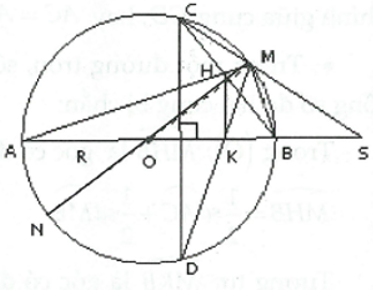
1) \(\Delta SBC\) và \(\Delta SMA\) có:
\(\widehat {BSC} = \widehat {MSA}\), \(\widehat {SCB} = \widehat {SAM}\) (góc nội tiếp cùng chắn )
\( \Rightarrow \Delta DBC\) đồng dạng với \(\Delta SMA\).
Nhận xét: Bài toán chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.
2) Vì \(AB \bot CD\) nên .
Suy ra: \(\widehat {MHB} = \widehat {MKB}\) (vì cùng bằng )
\( \Rightarrow \) Tứ giác BMHK nội tiếp được đường tròn \( \Rightarrow \widehat {HMB} + \widehat {HKB} = 180^\circ \). (1)
Lại có: \(\widehat {HMB} = \widehat {AMB} = 90^\circ \) (2) (góc nội tiếp chắn nửa đường tròn)
Từ (1) (2) suy ra \(\widehat {HKB} = 90^\circ \) do đó \(HK//CD\) (cùng vuông góc với AB).
Nhận xét: Bài toán chứng minh hai đường thẳng song song bằng cách chứng minh chúng cùng vuông góc với một đường thẳng thứ ba.
3) Vẽ đường kính MN suy ra .
Ta có:
Mà và nên \(\widehat {OSM} = \widehat {OMK}\)
\( \Rightarrow \Delta OSM\) đồng dạng với \(\Delta OMK\)
\( \Rightarrow \frac{{OS}}{{OM}} = \frac{{OM}}{{OK}} \Rightarrow OK.OS = {R^2}\)
Nhận xét: Bài toán chứng minh một đẳng thức bằng cách chứng minh tam giác đồng dạng.
Cho biểu thức: \[P = \left( {\frac{{4\sqrt x }}{{2 + \sqrt x }} + \frac{{8x}}{{4 - x}}} \right):\left( {\frac{{\sqrt x - 1}}{{x - 2\sqrt x }} - \frac{2}{{\sqrt x }}} \right)\] với \(x > 9\).
1) Rút gọn biểu thức P?
2) Tìm m để với mọi giá trị \(x > 9\) ta có \(m\left( {\sqrt x - 3} \right)P > x + 1\)
Cho x; y là hai số thực thỏa mãn \(xy + \sqrt {\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)} = 1\). Chứng minh rằng \(x\sqrt {1 + {y^2}} + y\sqrt {1 + {x^2}} = 0\).
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Một thửa ruộng hình chữ nhật, nếu tăng chiều dài thêm 2m, chiều rộng thêm 3m thì diện tích tăng thêm 100m2. Nếu giảm cả chiều dài và chiều rộng đi 2m thì diện tích giảm đi 68m2. Tính diện tích thửa ruộng đó.
2) Xác định a, b để đường thẳng \(\left( d \right):ax + b\) cắt trục tung tại điểm có tung độ bằng \( - 2\) và cắt đồ thị \(\left( P \right):y = \frac{1}{4}{x^2}\) tại điểm có hoành độ bằng 2.
1) Giải hệ phương trình \(\left\{ \begin{array}{l}\left( {2x + 3y - 2} \right)\left( {x - 5y - 3} \right) = 0\\x - 3y = 1\end{array} \right.\)
2) Giải phương trình: \(3\sqrt {x - 2} - \sqrt {{x^2} - 4} = 0\).
3) Cho phương trình \(\left( {2m - 1} \right){x^2} - 2mx + 1 = 0\). Tìm m để phương trình trên có nghiệm thuộc khoảng \(\left( { - 1;0} \right)\)?