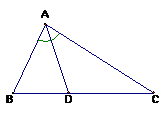
Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD.
a) Tính AD, DC.
b) Chứng minh .
c) Chứng minh AB.BI = BD.HB và tam giác AID cân.
Giải bởi Vietjack
a) Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
AB2 + AC2 = BC2
Ta có AD là tia phân giác , theo tính chất tia phân giác của tam giác:
.
Thay số, ta được: .
Þ DC = AC – AD = 8 – 3 = 5 (cm)
Vậy AD = 3 cm, DC = 5 cm.
b) Xét DHBA và DABC có:
(cùng phụ ).
Do đó DHBA 
DABC (g.g)
Suy ra: (1)
Mặt khác, BI là tia phân giác , áp dụng tính chất tia phân giác, ta có:
(2)
Từ (1) và (2) suy ra: (đpcm).
c) Xét DABD và DHBI có:
(vì BD là tia phân giác )
Do đó DABD 
DHBI (g.g)
Suy ra
Lại có DABD 
DHBI (hai góc tương ứng)
Mà: nên
Do đó DAID cân tại A.
Một xe khách và một xe tải xuất phát cùng một lúc đi từ tỉnh A đến tỉnh B. Mỗi giờ xe khách chạy nhanh hơn xe tải là 5km nên xe khách đến B trước xe tải 30 phút. Tính quãng đường AB, biết rằng vận tốc của xe tải là 40 km/h.
Giải các phương trình sau:
a) 3x − 12 = 0
b) (x – 2)(2x + 3) = 0
c) .
Trong hình vẽ, biết , theo tính chất đường phân giác của tam giác thì tỉ lệ thức nào sau đây là đúng?
