Một xe máy và một ô tô cùng khởi hành từ tỉnh A đi đến tỉnh B. Xe máy đi với vận tốc 30 km/h, ô tô đi với vận tốc 40 km/h. Sau khi đi được nửa quãng đường AB, ô tô tăng vận tốc thêm 5 km/h trên quãng đường còn lại, do đó nó đến tỉnh B sớm hơn xe máy 1 giờ 10 phút. Tính độ dài quãng đường AB.
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x là độ dài quãng đường AB (km) (x > 0).
Đổi 1 giờ 10 phút = ![]() giờ.
giờ.
Thời gian xe máy đi hết quãng đường AB là (giờ).
Thời gian ô tô đi nửa đầu quãng đường AB là: (giờ).
Vận tốc ô tô trên nửa sau quãng đường AB là: 40 + 5 = 45 (km/h).
Thời gian ô tô đi nửa sau quãng đường AB là: (giờ).
Do ô tô đến tỉnh B sớm hơn xe máy 1 giờ 10 phút nên ta có phương trình:
24x = 9x + 8x + 840
24x – 9x – 8x = 840
7x = 840
x = 120 (TMĐK).
Vậy độ dài quãng đường AB là 120 km.
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ∆AEB đồng dạng với ∆AFC. Từ đó suy ra AF . AB = AE . AC.
b) Chứng minh: .
c) Cho AE = 3 cm, AB = 6 cm. Chứng minh rằng SABC = 4SAEF.
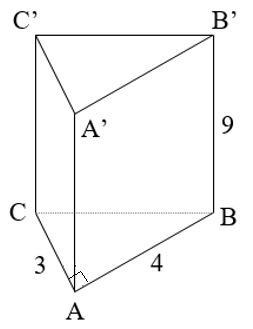
Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau:
Giải các phương trình và bất phương trình sau:
a) 2x – 3 = 0;
b) ;
c) .
Hình hộp chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm, chiều cao bằng 4 cm thì có thể tích là:
Nếu ∆ABC đồng dạng với ∆A’B’C’ theo tỉ số k thì ∆A’B’C’ đồng dạng với ∆ABC theo tỉ số nào?