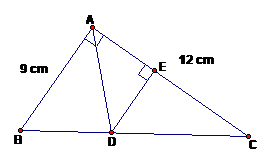
Cho tam giác ABC vuông tại A, biết AB = 9 cm và AC = 12 cm. Tia phân giác của góc BAC cắt cạnh BC tại điểm D. Từ D kẻ đường thẳng vuông góc với AC, đường thẳng này cắt AC tại E.
a) Chứng minh: ∆CED đồng dạng với ∆CAB.
b) Tính .
c) Tính diện tích tam giác ABD.
Giải bởi Vietjack
a)Xét ∆CED và ∆CAB có:
(vì )
chung
Do đó ∆CED 
∆CAB (g.g).
b) Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225.
Suy ra BC = 15 cm.
Vì ∆CED ∆CAB (cmt) nên .
Khi đó: .
Vậy .
c) Vì AD là tia phân giác của nên .
Khi đó .
Ta có: (cm2).
Mặt khác:
(cm2).
Vậy diện tích tam giác ABD là cm2.
Cho hai biểu thức:
và với x ≠ − 5, x ≠ − 1, x ≠ 4.
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức B tại x = 2.
c) Tìm giá trị nguyên của x để P = A . B đạt giá trị nguyên.
Giải bài toán bằng cách lập phương trình.
Số công nhân của hai xí nghiệp trước kia tỉ lệ với 3 và 4. Nay xí nghiệp I thêm 40 công nhân, xí nghiệp II thêm 80 công nhân. Do đó số công nhân hiện nay của hai xí nghiệp tỉ lệ với 8 và 11. Tính số công nhân của mỗi xí nghiệp hiện nay.
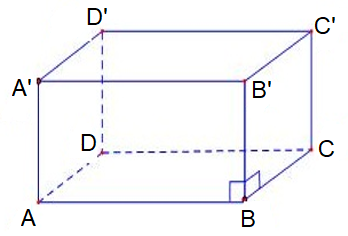
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (như hình vẽ). Tính thể tích của hình hộp chữ nhật. Biết AB = 5 cm, BC = 4 cm, CC’= 3 cm.
Giải các phương trình và bất phương trình sau:
a) ;
b) |x – 3| = 9 – 2x;
c) .
