Cho f(x) là hàm bậc 4 và có bảng biến thiên như hình vẽ sau
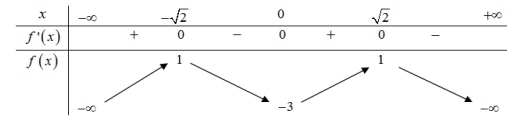
Đồ thị hàm số có mấy đường tiệm cận đứng
 Giải bởi Vietjack
Giải bởi Vietjack
Xét phương trình
Dựa vào BBT ta thấy:
Phương trình f(x) = -4 có 2 nghiệm phân biệt khác
Phương trình f(x) = 1 có 2 nghiệm kép bằng
Suy ra phương trình có 4 nghiệm phân biệt không bị triệt tiêu bởi nghiệm
Vậy đồ thị hàm số có 4 đường tiệm cận đứng.
Chọn B.Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Khoảng cách giữa 2 đường thẳng CD và SA là:
Gọi S là tập hợp các số tự nhiên có năm chữ số chia hết cho 5. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn chia hết cho 7 là
Biết hàm số y = 4sinx - 3 cosx + 2 đạt giá trị lớn nhất là M, giá trị nhỏ nhất là m. Tổng M + m là
Cho hàm số y = f(x) và y = g(x) có đồ thị tương ứng là hình 1 và hình 2 bên dưới:
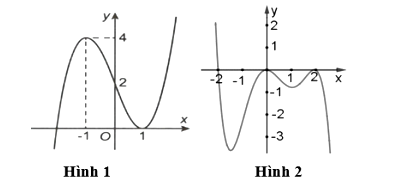
Số nghiệm không âm của phương trình là
Cho hàm số có đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ dương và đồ thị của hàm số y = f'(x) như hình vẽ:
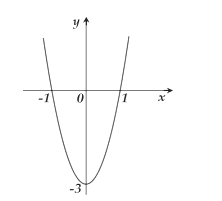
Giá trị lớn nhất của hàm số y = |f(x)| trên đoạn [0; 20] là:
Có bao nhiêu giá trị nguyên của tham số m (với |m| < 2021) để phương trình có nghiệm?
Cho hàm số y = f(x) có đạo hàm và f(0) = 1. Số điểm cực tiểu của hàm số là:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều và AA' = AB = a. Thể tích khối lăng trụ ABC.A'B'C' bằng
Cho hàm số f(x), hàm số có đồ thị như hình vẽ:
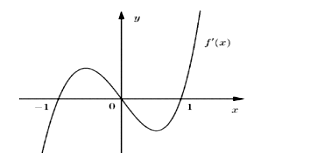
Hàm số có mấy khoảng đồng biến?