Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB . Gọi M là một điểm trên cạnh CD;(α) là mặt phẳng qua M và song song với SA và BC. Thiết diện của mp(α) với hình chóp là:
A.Hình tam giác
B.Hình thang
C.Hình bình hành
D.Hình chữ nhật
Giải bởi Vietjack
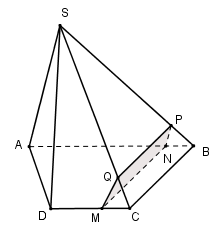
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{M \in (\alpha ) \cap (ABCD)}\\{BC\parallel (\alpha )}\\{BC \subset (ABCD)}\end{array}} \right. \Rightarrow (\alpha ) \cap (ABCD) = MN\parallel BC(N \in AB)\,\,(1)\)
Tương tự
\(\left\{ {\begin{array}{*{20}{c}}{N \in (\alpha ) \cap (SAB)}\\{SA\parallel (\alpha )}\\{SA \subset (SAB)}\end{array}} \right. \Rightarrow (\alpha ) \cap (SAB) = NP\parallel SA(P \in SB)\)
\(\left\{ {\begin{array}{*{20}{c}}{P \in (\alpha ) \cap (SBC)}\\{BC\parallel (\alpha )}\\{BC \subset (SBC)}\end{array}} \right. \Rightarrow (\alpha ) \cap (SBC) = PQ\parallel BC(Q \in SC)\,\,(2).\)
Từ (1) và (2) suy ra MN//PQ .
Vậy thiết diện là hình thang MNPQ.
Đáp án cần chọn là: B
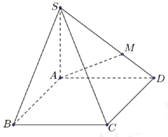
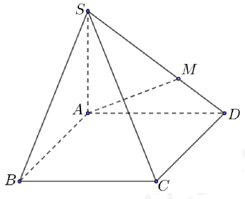
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi điểm M là điểm thuộc cạnh SD sao cho SM=\(\frac{2}{3}\)SD (minh họa như hình vẽ). Mặt phẳng chứa AM và song song với BD cắt cạnh SC tại K. Tỷ số \(\frac{{SK}}{{SC}}\) bằng
Cho hình lập phương ABCD.A′B′C′D′ cạnh aa. Các điểm M,N,P theo thứ tự đó thuộc các cạnh BB′,C′D′,DA sao cho \[BM = C\prime N = DP = \frac{a}{3}\]. Tìm diện tích thiết diện S của hình lập phương khi cắt bởi mặt phẳng (MNP).
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I,J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG)
Cho tứ diện đều ABCD cạnh a . Gọi M và P lần lượt là hai điểm di động trên các cạnh AD và BC sao cho \[MA = PC = x(0 < x < \frac{a}{2})\] . Mặt phẳng (α) đi qua MP song song với CD cắt tứ diện theo một thiết diện là hình gì?
Cho hình hộp ABCD.A′B′C′D′. Trên các cạnh AA′, BB′, CC′ lần lượt lấy ba điểm M, N, P sao cho \[\frac{{A'M}}{{{\rm{AA}}'}} = \frac{1}{3},\frac{{B'N}}{{BB'}} = \frac{2}{3},\frac{{C'P}}{{CC'}} = \frac{1}{2}\]. Biết mặt phẳng (MNP) cắt cạnh DD′ tại Q. Tính tỉ số \[\frac{{D'Q}}{{{\rm{DD}}'}}\]
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông tại A, \(SA = a\sqrt 3 ,SB = 2a\). Điểm M nằm trên đoạn AD sao cho AM=2MD. Gọi (P) là mặt phẳng qua M và song song với (SAB). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
Cho hình lập phương ABCD.A′B′C′D′,AC và BD cắt nhau tại O,A′C′ và B′D′ cắt nhau tại O′ . Các điểm M,N,P theo thứ tự là trung điểm của AB,BC,O′B′. Khi đó thiết diện do mặt phẳng (MNP) cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
Cho hình chóp S.ABCD, G là điểm nằm trong tam giác SCD. E, F lần lượt là trung điểm của AB và AD. Thiết diện của hình chóp khi cắt bởi mặt phẳng (EFG) là
Cho hình hộp ABCD.A′B′C′D′, gọi M là trung điểm CD, (P) là mặt phẳng đi qua M và song song với B′D và CD′. Thiết diện của hình hộp cắt bởi mặt phẳng (P) là hình gì?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, tam giác SBD cân tại S. Gọi M là điểm tùy ý trên AO. Mặt phẳng (α) đi qua M và song song với SA,BD cắt SO,SB,AB tại N,P,Q. Tứ giác MNPQ là hình gì?
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn BC , đáy nhỏ AD. Mặt bên (SAD) là tam giác đều, (α) là mặt phẳng đi qua M trên cạnh AB , song song với SA,BC. Mp(α)cắt các cạnh CD,SC,SB lần lượt tại N,P,Q.MNPQ là hình gì?
Cho tứ diện ABCD có AB=a, CD=b. Gọi I, J lần lượt là trung điểm AB và CD, giả sử AB⊥CD. Mặt phẳng (α) qua M nằm trên đoạn IJ và song song với AB và CD Tính diện tích thiết diện của tứ diện ABCD với mặt phẳng (α) biết \[IM = \frac{1}{3}IJ\].
Cho tứ diện ABCD có AB=6, CD=8. Cắt tứ diện bởi một mặt phẳng song song với AB, CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA=SD=3a, SB=SC=\(3a\sqrt 3 \). Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP=2a. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC) . Khẳng định nào sau đây là đúng?
