Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên SA=2a và vuông góc với mặt đáy (ABCD). Gọi H và K lần lượt là trung điểm của cạnh BC và CD. Tính khoảng cách giữa hai đường thẳng HK và SD.
A.\[\frac{a}{3}.\]
B. \[\frac{{2a}}{3}.\]
C. \[2a\]
D. \[\frac{a}{2}.\]
Giải bởi Vietjack
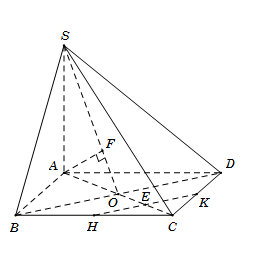
Gọi\[E = HK \cap AC.\] Do \[HK\parallel BD\] nên suy ra\[d\left( {HK;SD} \right) = d\left( {HK;\left( {SBD} \right)} \right) = d\left( {E;\left( {SBD} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBD} \right)} \right)\]
(vì \[OE = \frac{1}{2}AO\])
Kẻ \[AF \bot SO\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{BD \bot AC}\\{BD \bot SA}\end{array}} \right. \Rightarrow BD \bot (SAC) \Rightarrow BD \bot AF(2)\)
Từ (1) và (2) \[ \Rightarrow AF \bot \left( {SBD} \right)\] khi đó\[d\left( {A;\left( {SBD} \right)} \right) = AF = \frac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \frac{{2a.\frac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \frac{{{a^2}}}{2}} }} = \frac{{2a}}{3}.\]
Vậy khoảng cách\[d\left( {HK;SD} \right) = \frac{1}{2}AF = \frac{a}{3}.\]
Đáp án cần chọn là: A
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết mặt phẳng (SBC) tạo với đáy một góc 600 và M là trung điểm của SD. Tính khoảng cách d giữa hai đường thẳng AB và CM.
Cho tứ diện đều ABCD có cạnh bằng 2a. Khoảng cách giữa hai đường thẳng AB và CD là
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB=2a,AD=DC=a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 600. Tính khoảng cách d giữa hai đường thẳng AC và SB.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA=2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và đáy bằng 600. Gọi M là trung điểm của AC, tính khoảng cách dd giữa hai đường thẳng AB và SM.
Cho hình lăng trụ ABC.A′B′C′ có đáy là tam giác đều cạnh có độ dài bằng 2a. Hình chiếu vuông góc của A′A′ lên mặt phẳng (ABC) trùng với trung điểm H của BC. Tính khoảng cách d giữa hai đường thẳng BB′ và A′H.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với \(AC = \frac{{a\sqrt 2 }}{2}\). Cạnh bên SA vuông góc với đáy, SB hợp với đáy góc 600. Tính khoảng cách d giữa hai đường thẳng AD và SC.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với mặt phẳng đáy góc 450. Khoảng cách giữa hai đường thẳng SB và AC là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác SBC là tam giác đều cạnh aa và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và BC.
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh \(a\sqrt {2,} {\rm{AA}}' = 2a\). Tính khoảng cách dd giữa hai đường thẳng BD và CD′.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \sqrt 3 \). Tính khoảng cách d giữa hai đường thẳng SA và BD.
Cho hình lăng trụ đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :
Cho tứ diện gần đều ABCD, biết \[AB = CD = 5,AC = BD = \sqrt {34} ,AD = BC = \sqrt {41} \]. Tính sin của góc giữa hai đường thẳng AB và CD.
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác vuông cân, AC=BC=3a. Hình chiếu vuông góc của B′ lên mặt đáy trùng với trọng tâm của tam giác ABC, mặt phẳng (ABB′A′) tạo với mặt phẳng (ABC) một góc 600. Tính khoảng cách giữa hai đường thẳng AB và B′C.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, gọi I là trung điểm của AB. Hình chiếu vuông góc của S trên mặt đáy là trung điểm của CI. Biết chiều cao của khối chóp là \(a\sqrt 3 \). Khoảng cách giữa hai đường thẳng AB và SC là :
