Nếu một khối chóp có thể tích bằng a3 và diện tích mặt đáy bằng a2 thì chiều cao của khối chóp bằng:
A.2a
B.3a
C.\(\frac{a}{3}\)
D.a
Giải bởi Vietjack
Chiều cao của khối chóp đã cho là:
\[h = \frac{{3V}}{S} = \frac{{3{a^3}}}{{{a^2}}} = 3a.\]
Đáp án cần chọn là: B
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc 450. Gọi M,N lần lượt là trung điểm của AB và AD. Thể tích của khối chóp S.MCDN là:
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn \[SA \bot \left( {ABCD} \right)\;\] và \[AB = 2AD = 2CD = 2a = \sqrt 2 SA\]. Thể tích khối chóp S.BCD là:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
Cho hình chóp S.ABC, đáy là tam giác ABC có \[AB = BC\sqrt 5 ,\;AC = 2BC\sqrt 2 \], hình chiếu của S lên mặt phẳng (ABC) là trung điểm O của cạnh AC. Khoảng cách từ A đến mặt phẳng (SBC) bằng 2. Mặt phẳng (SBC) hợp với mặt phẳng (ABC) một góc α thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp S.ABC bằng \(\frac{{\sqrt a }}{b}\), trong đó \[a,b \in {\mathbb{N}^*},\;\]a là số nguyên tố. Tổng a+b bằng:
Phép vị tự tỉ \[k > 0\;\]biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
Thể tích khối bát diện đều cạnh a bằng:
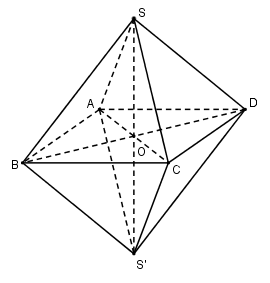
Thể tích khối bát diện đều\[V = 2{V_{S.ABCD}}\]
Gọi\[O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\]
Vì ABCD là hình vuông nên \[AC = BD = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\]
\[SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow {\rm{\Delta }}SOA\]vuông tại O
\[ \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}\]\[ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\]
\[ \Rightarrow V = 2\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{3}\]
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 600. Thể tích của khối chóp đó là:
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết SB=a,SC hợp với (SAB) một góc 300 và (SAC) hợp với đáy (ABC) một góc 600. Thể tích khối chóp là:
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và có thể tích \[V = \frac{{{a^3}\sqrt 3 }}{6}\]. Tìm số r>0 sao cho tồn tại điểm J nằm trong khối chóp mà khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r?
Cho tứ diện ABCD có G là điểm thỏa mãn \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]. Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số \[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\] là
Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau, AB=6a,AC=7a,AD=4a. Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CD,DB. Thể tích V của tứ diện AMNP là:
Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng 450, góc giữa SD và đáy bằng α với \[tan\alpha = \frac{1}{3}\]. Tính thể tích khối chóp đã cho.
