Cho mặt cầu tâm O bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón N có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h(h > R). Tìm hh để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
A.\[h = R\sqrt 3 \]
B. \[h = R\sqrt 2 \]
C. \[h = \frac{{4R}}{3}\]
D. \[h = \frac{{2R}}{3}\]
Giải bởi Vietjack
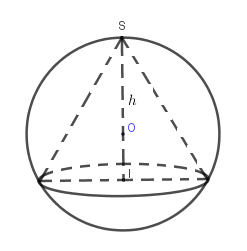
Ta có: Gọi bán kính (C) với tâm là I là r thì dễ có S phải thuộc OI và :
\[\begin{array}{*{20}{l}}{OI = \sqrt {{R^2} - {r^2}} \to h = \sqrt {{R^2} - {r^2}} + R}\\{V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {r^2}(\sqrt {{R^2} - {r^2}} + R)}\end{array}\]
Tới đây ta sẽ khảo sát hàm số:
\[f(r) = {r^2}(\sqrt {{R^2} - {r^2}} + R)\]
\[ = {r^2}\sqrt {{R^2} - {r^2}} + {r^2}R\]
\[ \Rightarrow f\prime (r) = ({r^2}\sqrt {{R^2} - {r^2}} + {r^2}R)\prime \]
\[ = \left( {{r^2}\sqrt {{R^2} - {r^2}} } \right)' + ({r^2}R)\prime \]
\[ = ({r^2})\prime \sqrt {{R^2} - {r^2}} + {r^2}(\sqrt {{R^2} - {r^2}} )\prime + 2rR\]
\[ = 2r\sqrt {{R^2} - {r^2}} + {r^2}.\frac{{ - 2r}}{{2\sqrt {{R^2} - {r^2}} }} + 2rR\]
\[ = 2r\sqrt {{R^2} - {r^2}} - \frac{{{r^3}}}{{\sqrt {{R^2} - {r^2}} }} + 2rR\]
\[ = r(2\sqrt {{R^2} - {r^2}} - \frac{{{r^2}}}{{\sqrt {{R^2} - {r^2}} }} + 2R)\]
\[\begin{array}{l}f'(r) = 0 \Leftrightarrow 2\sqrt {{R^2} - {r^2}} + 2{\rm{R}} - \frac{{{r^2}}}{{\sqrt {{R^2} - {r^2}} }} = 0\\ \Leftrightarrow 2({R^2} - {r^2}) - {r^2} + 2{\rm{R}}\sqrt {{R^2} - {r^2}} = 0\end{array}\]
\[ \Leftrightarrow {(2{{\rm{R}}^2} - 3{{\rm{r}}^2})^2} = {(2{\rm{R}}\sqrt {{R^2} - {r^2}} )^2}\]
\[ \Leftrightarrow {r^2} = \frac{8}{9}{R^2} \to h = \frac{{4{\rm{R}}}}{3}.\]
Đáp án cần chọn là: C
Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Cho tam giác AOB vuông tại O. Quay tam giác quanh cạnh OA ta được hình nón có đường sinh và đường cao lần lượt là:
Cho tam giác ABC đều, có diện tích bằng s1 và AH là đường cao. Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có diện tích xung quanh bằng s2. Tính \(\frac{{{s_1}}}{{{s_2}}}\).
Cho hai đường thẳng d và d′ cắt nhau tại điểm O và góc giữa hai đường thẳng là \[\alpha ({0^0} < \alpha < {90^0}).\] Quay đường thẳng d′ quanh d thì ta được mặt nón có góc ở đỉnh bằng:
Hình nón có thiết diện qua trục là tam giác đều cạnh a = 3 . Tính độ dài đường cao của hình nón.
Cho hình nón đỉnh S có bán kính đáy R = 2. Biết diện tích xung quanh của hình nón là \[2\sqrt 5 \pi \]. Tính thể tích khối nón.
Cho hai đường thẳng d và d′ cắt nhau tại điểm O và góc giữa hai đường thẳng là \[\alpha \]. Quay đường thẳng d′ quanh d thì số đo \[\alpha \] bằng bao nhiêu để mặt tròn xoay nhận được là mặt nón tròn xoay?
Công thức tính thể tích khối nón có bán kính đáy r, độ dài đường sinh l và chiều cao h là:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD,BC; AD = 3BC = 3a, AB = a,\(SA = a\sqrt 3 \). Điểm I thỏa mãn \(\overrightarrow {AD} = 3\overrightarrow {AI} \); M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng(ABCD).
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
Cho hình nón bán kính đáy r và diện tích xung quanh Sxq. Độ dài đường sinh l của hình nón là:
Diện tích xung quanh hình nón có bán kính đáy r = 3cm và độ dài đường sinh 4cm là:
