Gọi \(S\) là tập hợp tất cả các giá trị nguyên \(m\) để đồ thị hàm số \(y = \left| {3{x^4} - 8{x^3} - 6{x^2} + 24x - m} \right|\) có 7 điểm cực trị. Tính tổng các phần tử của \(S\).
A. 30
B. 50
C. 63
D. 42
Giải bởi Vietjack
Đáp án D
Phương pháp giải:
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) với \(f\left( x \right)\) là hàm đa thức = số điểm cực trị của hàm số \(y = f\left( x \right)\) + số giao điểm (không tính điểm tiếp xúc) của đồ thị hàm số \(f\left( x \right)\) và trục hoành.
Giải chi tiết:
Xét hàm số \(f\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x - m\)
Đồ thị hàm số \(f\left( x \right)\) có nhiều nhất 3 điểm cực trị và cắt trục hoành tại nhiều nhất 4 điểm.
Do đó để đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có 7 điểm cực trị thì đồ thị hàm số \(f\left( x \right)\) phải cắt trục hoành tại 4 điểm phân biệt và có 3 điểm cực trị.
\( \Rightarrow \) đồ thị hàm số \(f\left( x \right)\) phải cắt trục hoành tại 4 điểm phân biệt (vì khi đó chắc chắn hàm số \(y = f\left( x \right)\) sẽ có 3 điểm cực trị) \( \Rightarrow \) Phương trình \(3{x^4} - 8{x^3} - 6{x^2} + 24x - m = 0 \Leftrightarrow 3{x^4} - 8{x^3} - 6{x^2} + 24x = m{\mkern 1mu} {\mkern 1mu} \left( * \right)\) phải có 4 nghiệm phân biệt.
Xét hàm số \(g\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x\) ta có \(g'\left( x \right) = 12{x^3} - 24{x^2} - 12x + 24 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\\{x = 2}\end{array}} \right.\)
BBT:
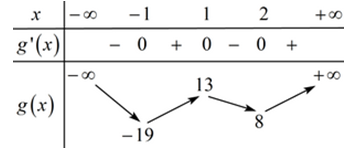
Dựa vào BBT ta thấy phương trình (*) có 4 nghiệm phân biệt \( \Leftrightarrow 8 < m < 13\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in S = \left\{ {9;10;11;12} \right\}\)
Vậy tổng tất cả các phần tử của \(S\) là \(9 + 10 + 11 + 12 = 42\).
Ông \(A\) dự định sử dụng hết \(6,5{m^3}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Cho \(f\left( x \right)\) là một đa thức thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{x - 2}} = 3\). Tính \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{\left( {{x^2} - 4} \right)\left( {\sqrt {2f\left( x \right) + 6} + 3} \right)}}\).
Nêu ý nghĩa của hai câu thơ:
"Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm”
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: "Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự... thế giới cùng anh em chiến hữu...".
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễnhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta...
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Nội dung chính của văn bản trên là gì?
Bệnh bạch tạng ở người do đột biến gen lặn a nằm trên nhiễm sắc thể thường quy định, alen trội A tương ứng quy định người bình thường. Một gia đình có bố và mẹ bình thường nhưng người con đầu của họ bị bạch tạng. Khả năng để họ sinh đứa con thứ hai cũng bị bệnh bạch tạng là bao nhiêu?
Anh/Chị hiểu như thế nào về câu nói: “Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.”
Một xạ thủ bắn bia. Biết rằng xác suất bắn trúng vòng 10 là 0,2; vòng 9 là 0,25 và vòng 8 là 0,15. Nếu trúng vòng nào thì được số điểm tương ứng với vòng đó. Giả sử xạ thủ bắn 3 phát súng một cách độc lập. Xạ thủ đạt loại giỏi nếu được ít nhất 28 điểm. Tính xác suất để xạ thủ đạt loại giỏi.
Trong thí nghiệm khe Young ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm A, B đối xứng qua vân trung tâm, khi màn cách hai khe một khoảng là D thì A, B là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng dd thì A, B là vân sáng và đếm được số vân sáng trên đoạn AB trước và sau khi dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoảng 9d nữa thì A, B lại là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại A và B không còn xuất hiện vân sáng nữa. Tại A khi chưa dịch chuyển màn là vân sáng thứ mấy?
Cho các chất sau tan trong nước: Na2CO3, CH3COOCH3, HCOOH, MgCl2, HF. Số chất điện li mạnh và điện li yếu lần lượt là
Cho các ý sau:
1. Ức chế sinh trưởng của chồi đỉnh.
2. Kích thích sinh trưởng của các chồi bên.
3. Tạo ưu thế đỉnh cho cây..
Khi trồng các loại hoa màu, người ta thường ngắt bỏ ngọn bí, mướp, dưa, …. Việc này có tác dụng:
Chỉ ra biện pháp tu từ chính được sử dụng trong câu: “Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh”.
Theo giả thuyết siêu trội, phép lai nào sau đây cho đời con có ưu thế lai cao nhất?
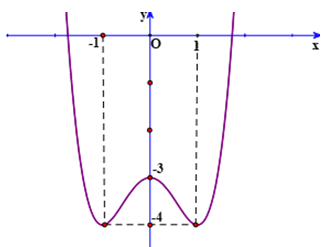
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Tìm \[m\] để phương trình \[f\left( {\sin x} \right) = m\] có đúng hai nghiệm trên đoạn \[\left[ {0;\pi } \right]\].
