Một lớp có 38 học sinh, trong đó có 20 học sinh nam. Chọn ngẫu nhiên một học sinh. Tính xác suất để chọn được một học sinh nữ.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
Xét phép thử: “Chọn ngẫu nhiên một học sinh từ 38 học sinh trong lớp”
Gọi biến cố A: “Chọn được một học sinh nữ”
Trong lớp có 18 học sinh nữ, nên có (cách) chọn một học sinh nữ.
Vậy
Biết giá trị lớn nhất của hàm số trên đoạn [0; 2] bằng 5, tìm giá trị của tham số m
Cho hàm số f(x) có bảng xét dấu của đạo hàm f'(x) như sau:
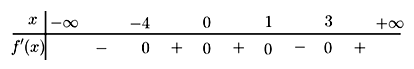
Số điểm cực trị của hàm số f(x) đã cho là:
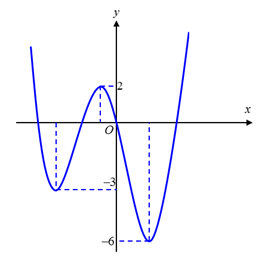
Cho hàm số f(x) liên tục trên và đồ thị hàm số y = f(x) cắt trục hoành tại các điểm có hoành độ lần lượt là (như hình bên dưới). Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên [a; c] bằng 2021. Tổng tất cả các phần tử của S bằng:
Trong không gian Oxyz, cho hai điểm Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
Một xí nghiệp chế biến sữa bò muốn sản xuất lon đựng sữa có dạng hình trụ bằng thiếc có thể tích không đổi. Để giảm giá một lon sữa khi bán ra thị trường người ta cần chế tạo lon sữa có kích thước sao cho ít tốn kém vật liệu. Để thỏa mãn yêu cầu đặt ra (diện tích toàn phần bé nhất), người ta phải thiết kế lon sữa thỏa mãn điều kiện nào trong các điều kiện sau:
Trong không gian tọa độ Oxyz, cho ba điểm và C(0; 2; 3). Trọng tâm G của tam giác ABC có tọa độ là:
Cho hàm số bậc bốn f(x) thỏa mãn và đồ thị y = f'(x) (như hình vẽ bên dưới).
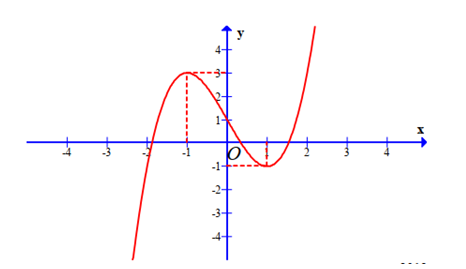
Xét hàm số f(x) thỏa mãn và Tìm số nghiệm của phương trình g'(x) = 0.
Gọi A, B, C là 3 điểm có hoành độ thỏa mãn và tung độ bằng nhau, lần lượt thuộc đồ thị hàm số Tính độ dài đoạn thẳng AB?
Cho hàm số f(x) có bảng biến thiên như sau:
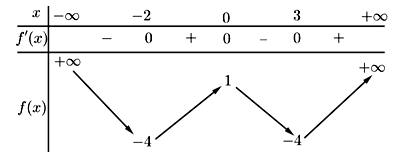
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?