Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của là:
A.
B.
C.
D.
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
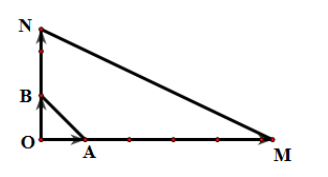
Dựng điểm M, N sao cho và . Khi đó ta có:
.
Từ dữ kiện .
Ta suy ra cùng phương với .
Vì có cùng điểm đầu là O.
Nên giá của trùng nhau.
Do đó ta có OM ≡ OA.
Tương tự ta có ON ≡ OB.
Mà OA ⊥ OB (tam giác OAB vuông cân tại O).
Do đó OM ⊥ ON.
Ta có .
Tương tự, ta có .
Tam giác OMN vuông tại O: (Định lý Pytago)
.
Vậy ta chọn đáp án D.
Cho hình bình hành ABCD tâm O và điểm M bất kỳ. Khẳng định nào sau đây đúng?
Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?
Cho ba điểm phân biệt A, B, C. Nếu thì đẳng thức nào dưới đây đúng?
Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức .
Cho hình bình hành ABCD, điểm M thỏa mãn . Xác định vị trí điểm M.
Cho tam giác ABC. Gọi M là trung điểm BC và N là trung điểm AM. Đường thẳng BN cắt AC tại P. Khi đó thì giá trị của x là:
Cho tam giác ABC có điểm O thỏa mãn . Khẳng định nào sau đây là đúng?
Cho tam giác ABC và một điểm M tùy ý. Cho . Hãy xác định vị trí của điểm D sao cho .
Cho và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn và . Tìm .
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó bằng
