Cho tam giác nhọn ABC, AH là đường cao, D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng:
Giải bởi Vietjack
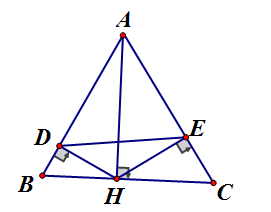
a) vuông tại H, HD là đường cao, áp dụng hệ thức lượng
chứng minh tương tự ta có
Từ (1) và (2) suy ra
b) Từ
Xét và có: chung
(hai góc tương ứng)
Cho hình thoi ABCD với Tia Ax tạo với tia bằng và cắt cạnh BC tại M, cắt đường thẳng CD tại N.
Chứng minh rằng:
Cho đoạn thẳng AB = 4cm, C là điểm di động sao cho BC = 3cm. Vẽ tam giác AMN vuông tại A có AC là đường cao. Xác định vị trí điểm C để đạt giá trị lớn nhất.
Cho tam giác DEF vuông tại D, đường cao DH, đường trung tuyến DM, DF = 16cm, EF = 20cm, Tính:
Cho tam giác ABC vuông tại A, AH là đường cao. Cho biết BH = x, HC = y. Chứng minh rằng:
Cho tam giác ABC vuông tại A, đường cao AH, biết rằng BH = 25cm, CH = 144cm. Tính
Một tam giác vuông có cạnh huyền là 5, và đường cao ứng với cạnh huyền là 2. Tính hai cạnh góc vuông.
