Cho tam giác ABC nhọn các đường cao BD, CE cắt nhau tại H
a) CMR: B, E, D, C cùng thuộc một đường tròn
b) CMR: A, D, H, E cùng thuộc một đường tròn
c) CMR:
Giải bởi Vietjack
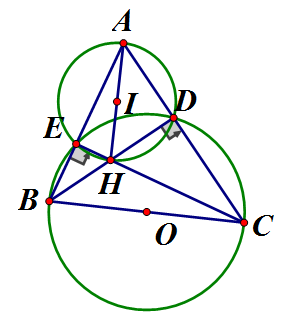
Gọi I là trung điểm AH. Theo tính chất đường trung tuyến trong tam giác vuông
đường trong (I; IA)
Trong (O) ta có BC là đường kính, DE là dây cung
Trong (I) ta có AH là đường kính, DE là dây cung nên
Cho đường tròn (O; R) và một dây cung AB. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M
a) Cho Tính độ dài dây cung MA
b) Gọi N là điểm đối xứng của M qua O, giả sử Tính bán kính R.
Cho đường tròn (O; R), A và B di động trên đường tròn (O) thỏa mãn Vẽ tại H
a) Chứng minh H là trung điểm của AB
b) Tính OH, AB. Diện tích theo R
c) Tia OH cắt (O; R) tại C. Tứ giác OACB là hình gì ? Vì sao ?
Cho hai hàm số và Chứng minh rằng:
a) Hàm số là các hàm số đồng biến
b) Hàm số f(x) - g(x) là hàm số nghịch biến.
Cho đường tròn (O; R), A và B thuộc (O) sao cho Gọi M là trung điểm AB.
a) Chứng minh
b) Tính độ dài AB, OM theo R
