Cho tam giác đều ABC cạnh a. Tính:.
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C.
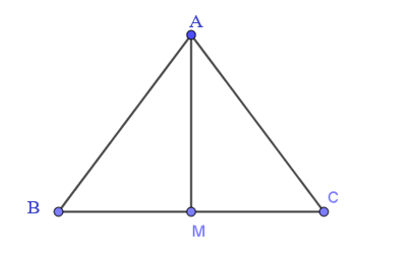
Gọi M là trung điểm của BC.
Do đó ta có:
Khi đó: (hiệu hai vectơ)
.
Do tam giác ABC đều nên AM vừa là trung tuyến vừa là đường cao nên tam giác AMB vuông tại M.
Ta có: BM = .
Áp dụng định lí Pythagore ta có:
AB2 = AM2 + BM2 ⇔ AM2 = AB2 – BM2 = a2 – =
Vậy .
Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ .
Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: .
