Cho nửa đường tròn đường kính AB. Có AC và BD là hai dây thuộc nửa đường tròn cắt nhau tại E. Đẳng thức nào sau đây là đúng ?
A.
B.
C.
D.
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A.
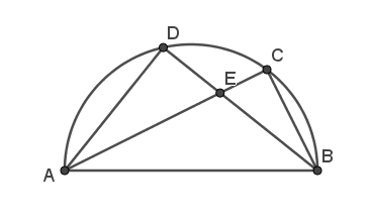
Vì AB là đường kính nên ,
Do đó AD ⊥ BD và AC ⊥ BC hay AD ⊥ BE và AE ⊥ BC.
Suy ra
Ta có:
(luôn đúng)
Cho tam giác ABC có trọng tâm G. Khẳng định nào sau đây là đúng ?
Cho tam giác ABC có trực tâm H. Gọi M là trung điểm BC. Đẳng thức nào sau đây là đúng ?
Cho tam giác ABC có BC = a, CA = b, AB = c. Trên cạnh AB lấy điểm M. Khẳng định nào sau đây là đúng ?
Cho tam giác đều ABC cạnh bằng a và O là trọng tâm tam giác. Tập hợp tất cả các điểm M là đường tròn tâm O bán kính . Khẳng định nào sau đây là đúng ?
Cho tam giác ABC có trực tâm H và trung điểm cạnh BC là M. Khẳng định nào sau đây là đúng ?
Cho tứ giác ABCD có AC vuông góc với BD. Đẳng thức nào sau đây là đúng ?
Cho MN là một đường kính bất kì của đường tròn tâm O bán kính R. Cho A là một điểm cố định và OA = d. Đẳng thức nào sau đây đúng?
Cho tam giác ABC có trọng tâm G. Gọi G’ là hình chiếu của trọng tâm G trên cạnh BC, biết điểm M nằm trong tam giác ABC sao cho M’ là hình chiếu của M trên BC và 3M’G’ = BC. Đẳng thức nào dưới đây là đúng ?
Cho hai điểm A, B và O là trung điểm của AB. Gọi M là một điểm tùy ý, khẳng định nào sau đây là đúng ?
