Tìm tất cả các giá trị của m để bất phương trình mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ
A. m = 0;
B. m < 0;
C. 0 < m ≤ \(\frac{1}{2}\);
D. m ≥ \(\frac{1}{2}\);
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Đặt f(x) = mx2 – x + m là tam thức bậc hai với a = m, b = – 1 và c = m
Với m = 0 thì f(x) = – x , f(x) ≥ 0 ⇔ – x ≥ 0 ⇔ x ≤ 0. Vậy m = 0 không thỏa mãn.
Với m ≠ 0 thì f(x) = mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta = {1^2} - 4.m.m \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\1 - 4{m^2} \le 0\end{array} \right.\)
Xét f(m) = 1 – 4m2 có ∆ = 16 > 0, hai nghiệm phân biệt là x = \( - \frac{1}{2}\); x = \(\frac{1}{2}\) và a = – 4 < 0. Ta có bảng xét dấu
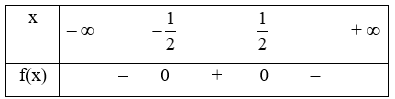
Từ bảng xét dấu ta có để 1 – 4m2 ≤ 0 thì m\( \in \left( { - \infty ; - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\)
Vậy để mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m \le - \frac{1}{2}\\m \ge \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \ge \frac{1}{2}\)
Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Trong các tập hợp sau, tập nào không là tập con của S?
Tìm tất cả các giá trị của m để bất phương trình x2 – x + m ≤ 0 vô nghiệm?
Các giá trị m để bất phương trình x2 – (m + 2)x + 8m + 1 < 0 luôn có nghiệm
Cho phương trình x2 – 2x – m = 0. Tìm tất cả các giá trị của m để phương trình có 2 nghiệm thỏa mãn x1 < x2 < 2.
Cho bất phương trình x2 – (2m + 2)x + m2 + 2m < 0. Tìm m để bất phương trình nghiệm đúng với mọi x thuộc đoạn [0; 1]
Cho bất phương trình mx2 – (2m – 1)x + m + 1 < 0(1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
Xác định m để (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ