Giả sử A và B là hai điểm phân biệt trên đường tròn (O). Các tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại điểm M. Từ A kẻ đường thẳng song song với MB cắt đường tròn (O) tại C. MC cắt đường tròn (O) tại E. Các tia AE và MB cắt nhau tại K.
Chứng minh rằng và .
Giải bởi Vietjack
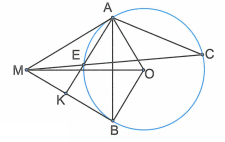
Do MB song song với AC nên (hai góc so le trong).
Ta lại có (cùng chắn ).
Do đó .
Xét và có: (chứng minh trên).
chung.
Suy ra (đpcm). (1)
Ta thấy (cùng chắn ).
Từ đó . (2)
Từ (1) và (2) suy ra nghĩa là (đpcm).
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường tròn (O') tại D. Vẽ đường tròn (I) qua ba điểm A,C,D cắt đường thẳng AB tại một điểm thứ hai là E. Chứng minh rằng:
a) .
