Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M,N lần lượt là điểm chính giữa của cung nhỏ AB và AC Gọi I là giao điểm BN và CM, dây MN cắt AB và AC lần lượt tại H và K
a, Chứng minh tứ giác BNHI nội tiếp
 Giải bởi Vietjack
Giải bởi Vietjack
a,
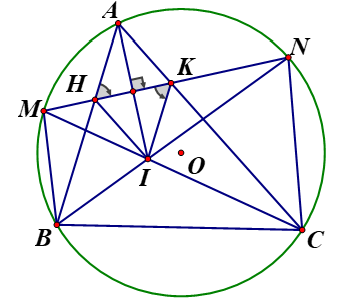
Ta có: (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)
Tứ giác BMHI là tứ giác nội tiếp (tứ giác có 2 đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau:
Cho hai phương trình: và . Để hai phương trình cùng vô số nghiệm thì:
Cho đường tròn (O;R) và một dây cung AB= R . Khi đó số đo cung nhỏ AB là
Cho phương trình x- 2y =2 (1) Phương trình nào sau đây kết hợp với (1) để được hệ phương trình vô số nghiệm
Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau: