22 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 28

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 28

3252 lượt thi
22 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Điều kiện để hàm số $y = (- m + 3) x - 3$ đồng biến trên R là:

A. m=3

B. $m < 3$

C. m>3

D. $m \neq 3$

Xem đáp án

Chọn đáp án B

Câu 2:

Cho hàm số

y = - 3 x^{2}

. Kết luận nào đúng

$A . y = 0 l à g i á t r ị l ớ n n h ấ t c ủ a h à m s ố$

$B . y = 0 l à g i á t r ị n h ỏ n h ấ t c ủ a h à m s ố$

$C . K h ô n g x á c đ ị n h đ ư ợ c g i á t r ị l ớ n n h ấ t c ủ a h à m s ố$

$D . X á c đ ị n h đ ư ợ c g i á t r ị n h ỏ n h ấ t c ủ a h à m s ố t r ê n$

Xem đáp án

Chọn đáp án A

Câu 3:

Điều kiện xác định của biểu thức $\sqrt{2019 - \frac{2019}{x}}$ là:

A, $x \neq 0$

B. $x \geq 1$

C. $x \geq 1$ hoặc x <0

D. $0 < x \leq 1$

Xem đáp án

Chọn đáp án C

Câu 4:

Cho phương trình x- 2y =2 (1) Phương trình nào sau đây kết hợp với (1) để được hệ phương trình vô số nghiệm

A. $2 x - 3 y = 3$

B. $2 x - 4 y = - 4$

C. $- \frac{1}{2} x + y = - 1$

D. $\frac{1}{2} x - y = - 1$

Xem đáp án

Chọn đáp án C

Câu 5:

Biểu thức $\sqrt{{(\sqrt{5} - 3)}^{2}} - \sqrt{5}$ có kết quả là:

A. $3 + 2 \sqrt{5}$

B. $3 - 2 \sqrt{5}$

C. $2 - 3 \sqrt{5}$

D. -3

Xem đáp án

Chọn đáp án B

Câu 6:

Cho hai phương trình: $x^{2} - 2 x + a = 0$ và $x^{2} + x + 2 a = 0$ . Để hai phương trình cùng vô số nghiệm thì:

A. a>1

B. a< 1

C. $a > \frac{1}{8}$

D. $a < \frac{1}{8}$

Xem đáp án

Chọn đáp án A

Câu 7:

Cho đường tròn (O;R) và một dây cung AB= R . Khi đó số đo cung nhỏ AB là

A. $60^{0}$

B. $120^{0}$

C. $150^{0}$

D. $100^{0}$

Xem đáp án

Chọn đáp án A

Câu 8:

Đường tròn là hình

A. Không có trục đối xứng

B. Có 2 trục đối xứng

C. Có 1 trục đối xứng

D. Có vô số trục đối xứng

Xem đáp án

Chọn đáp án D

Câu 9:

Cho phương trình

x^{2} - x - 4 = 0

có nghiệm x1, x2, biểu thức

A = x_{1}^{2} + x_{2}^{2}

có giá trị

A. A=28

B. A= -13

C. A= 13

D. A=18

Xem đáp án

Chọn đáp án C

Câu 10:

Thể tích hình cầu thay đổi như thế nào nếu bán kính tăng 2 lần

A. Tăng gấp 16 lần

B. Tăng gấp 8 lần

C. Tăng gấp 4 lần

D. Tăng gấp 2 lần

Xem đáp án

Chọn đáp án B

Câu 11:

Diện tích hình tròn ngoại tiếp tam giác đều cạnh a là:

A. $π a^{2}$

B. $\frac{3 π a^{2}}{4}$

C. $3 π a^{2}$

D. $\frac{π a^{2}}{3}$

Xem đáp án

Chọn đáp án D

Câu 12:

Cho tam giác ABC vuông tai A. Khi đó khẳng định đúng là :

A. $\frac{A B}{A C} = \frac{\cos C}{\cos B}$

B. $\sin B = \cos C$

C. $\sin B = \tan C$

D. $\tan B = \cos C$

Xem đáp án

Chọn đáp án B

Câu 13:

Rút gọn biểu thức sau : $A = \frac{4 + \sqrt{8} + \sqrt{2} - \sqrt{3} - \sqrt{6}}{2 + \sqrt{2} - \sqrt{3}}$

Xem đáp án

$\begin{array}{l} A = \frac{4 + \sqrt{8} + \sqrt{2} - \sqrt{3} - \sqrt{6}}{2 + \sqrt{2} - \sqrt{3}} \\ = \frac{4 + 2 \sqrt{2} + \sqrt{2} - \sqrt{3} - \sqrt{6}}{2 + \sqrt{2} - \sqrt{3}} = \frac{4 + 2 \sqrt{2} + \sqrt{2} - \sqrt{3} - \sqrt{2.3}}{2 + \sqrt{2} - \sqrt{3}} \\ = \frac{4 + 3 \sqrt{2} - \sqrt{3} - \sqrt{2} . \sqrt{3}}{2 + \sqrt{2} - \sqrt{3}} = \frac{(2 + \sqrt{2} - \sqrt{3}) + (2 \sqrt{2} + 2 - \sqrt{2.3})}{2 + \sqrt{2} - \sqrt{3}} \\ = \frac{2 + \sqrt{2} - \sqrt{3}}{2 + \sqrt{2} - \sqrt{3}} + \frac{\sqrt{2} . (2 + \sqrt{2} - \sqrt{3})}{2 + \sqrt{2} - \sqrt{3}} = 1 + \sqrt{2} \end{array}$

Câu 14:

Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau: $a) 5 x^{2} + 13 x - 6 = 0$

Xem đáp án

a, $5 x^{2} + 13 x - 5 = 0$

$Δ = 13^{2} + 4.5.6 = 289 > 0 \Rightarrow \sqrt{Δ} = \sqrt{289} = 17$

Phương trình có hai nghiệm phân biệt : $\{\begin{cases} x_{1} = \frac{- 13 + 17}{2.5} = \frac{2}{5} \\ x_{2} = \frac{- 13 - 17}{2.5} = - 3 \end{cases}$

Vậy phương trình có tập nghiệm $S = \{- 3; \frac{2}{5}\}$

Câu 15:

Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau:

b, $x^{4} + 2 x^{2} - 15 = 0$

Xem đáp án

b, $x^{4} + 2 x^{2} - 15 = 0$

Đặt $x^{2} = t (t \geq 0)$ , khi đó ta có phương trình

$\begin{array}{l} t^{2} + 2 t - 15 = 0 \Leftrightarrow t^{2} + 5 t - 3 t - 15 = 0 \\ \Leftrightarrow t (t + 5) - 3 (t + 5) = 0 \Leftrightarrow (t - 3) (t + 5) = 0 \\ \Leftrightarrow [\begin{array}{l} t = 3 (t m) \\ t = - 5 (k t m) \end{array} \Leftrightarrow x = \pm \sqrt{3} \end{array}$

Vậy phương trình đã cho có tập nghiệm $S = \{\pm \sqrt{3}\}$

Câu 16:

Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau: $c) \{\begin{cases} 3 x - 4 y = 17 \\ 5 x + 2 y = 11 \end{cases}$

Xem đáp án

c, $c) \{\begin{cases} 3 x - 4 y = 17 \\ 5 x + 2 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} 3 x - 4 y = 17 \\ 10 x + 4 y = 22 \end{cases} \Leftrightarrow \{\begin{cases} 13 x = 39 \\ 5 x + 2 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = - 2 \end{cases}$

Vậy hệ phương trình đã cho có nghiệm duy nhất $(x, y) = (3; - 2)$

Câu 17:

a, Trong mặt phẳng tọa độ Oxy vẽ parabol $y = \frac{1}{2} x^{2}$

Xem đáp án

a, Học sinh tự vẽ đồ thị parabol

Câu 18:

b, Tìm m để đường thẳng $(d) : y = (m - 1) x + \frac{1}{2} m^{2} + m$ đi qua điểm $M (1; - 1)$

Xem đáp án

b, Ta có điểm $M (1; - 1) \in (d) : y = (m - 1) x + \frac{1}{2} m^{2} + m$ , thay vào ta được

$\begin{array}{l} - 1 = (m - 1) .1 + \frac{1}{2} m^{2} + m \Leftrightarrow \frac{1}{2} m^{2} + m - 1 + 1 = 0 \\ \Leftrightarrow \frac{1}{2} m^{2} + 2 m = 0 \Leftrightarrow \frac{1}{2} m (m + 4) = 0 \\ \Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 4 \end{array} \end{array}$

Vậy $m = 0, m = - 4$ thỏa mãn bài toán.

Câu 19:

Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M,N lần lượt là điểm chính giữa của cung nhỏ AB và AC Gọi I là giao điểm BN và CM, dây MN cắt AB và AC lần lượt tại H và K

a, Chứng minh tứ giác BNHI nội tiếp

Xem đáp án

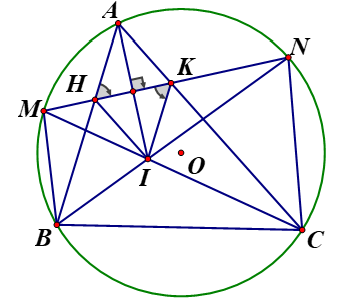
Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. (ảnh 1)

Ta có: $\hat{A B N} = \hat{N M C}$ (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)

$\Rightarrow \hat{H B I} = \hat{H M I} \Rightarrow$ Tứ giác BMHI là tứ giác nội tiếp (tứ giác có 2 đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).

Câu 20:

b,Chứng minh MK. MN = MI. MC

Xem đáp án

b, Ta có $\hat{M N B} = \hat{A C M}$ (hai góc chắn hai cùng bằng nhau) $\Rightarrow \hat{M N I} = \hat{M C K}$

Xét $Δ M I N$ và $Δ M K C$ có: $\hat{N M C}$ chung; $\hat{M N I} = \hat{M C K} (c m t)$

\Rightarrow Δ M I N ~ Δ M K C (g . g) \Rightarrow \frac{M I}{M N} = \frac{M K}{M C} \Rightarrow M K . M N = M I . M C (d f c m)

Câu 21:

c, Chứng minh tam giác AKI cân tại K

Xem đáp án

c, Ta có: $\hat{M N I} = \hat{M C K} (c m t) \Rightarrow$ Tứ giác NCIK là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

$\Rightarrow \hat{H K I} = \hat{N C I} = \hat{N C M}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)

Ta có: $\hat{N M C} = \frac{s d \overset{⏜}{M N}}{2}$ (góc nội tiếp bằng nửa số đo cung bị chắn)

$\hat{A H N} = \frac{s d \overset{⏜}{A N} + s d \overset{⏜}{B M}}{2} = \frac{s d \overset{⏜}{A N} + s d \overset{⏜}{A M}}{2} = \frac{s d \overset{⏜}{M N}}{2}$ (góc có đỉnh bên ngoài đường tròn) $\Rightarrow \hat{N C M} = \hat{A H K} \Rightarrow \hat{H K I} = \hat{A H K}$

Mà hai góc này ở vị trí so le trong $\Rightarrow A H / / K I$

Chứng minh hoàn toàn tương tự ta có $\hat{A K H} = \hat{K H I} \Rightarrow A K / / H I$

Xét tứ giác AHIK có:

\{\begin{cases} A H / / K I \\ A K / / H I \end{cases} \Rightarrow

Tứ giác AHIK là hình bình hành (1)

Tứ giác BMHI là tứ giác nội tiếp $\Rightarrow \hat{M H B} = \hat{M I B}$ (hai góc nội tiếp cùng chắn $\overset{⏜}{M B})$

Tứ giác NCIK là tứ giác nội tiếp $\Rightarrow \hat{N K C} = \hat{K I C}$ (hai góc nội tiếp cùng chắn $\overset{⏜}{N C})$

Mà $\hat{M I B} = \hat{N I C}$ (đối đỉnh) $\Rightarrow \hat{M H B} = \hat{N K I}$

$\hat{A H K} = \hat{A K H} (\hat{M H B} = \hat{A H K}, \hat{N K C} = \hat{A K H}$ đối đỉnh)

$\Rightarrow Δ A H K$ cân tại H $\Rightarrow A H = A K (2)$

Từ (1) và (2) $\Rightarrow A H I K$ là hình thoi $\Rightarrow K A = K I$

Vậy tam giác AKI cân tại K $(d f c m)$

Câu 22:

Với $x \neq 0,$ tìm giá trị nhỏ nhất của biểu thức $A = \frac{x^{2} - 3 x + 2019}{x^{2}}$

Xem đáp án

Điều kiện $x \neq 0$

Ta có $A = \frac{x^{2} - 3 x + 2019}{x^{2}} = 1 - \frac{3}{x} + \frac{2019}{x^{2}}$

Đặt $t = \frac{1}{x} (t \neq 0)$ , khi đó ta có:

$\begin{array}{l} A = 1 - 3 t + 2019 t^{2} = 2019 (t^{2} - \frac{1}{673} t) + 1 \\ = 2019 [t^{2} - 2 t . \frac{1}{1346} + {(\frac{1}{1346})}^{2}] - 2019. {(\frac{1}{1346})}^{2} + 1 \\ = 2019 {(t - \frac{1}{1346})}^{2} + \frac{2689}{2692} \end{array}$

Ta có:

$\begin{array}{l} {(t - \frac{3}{4038})}^{2} \geq 0 \forall t \Leftrightarrow 2019. {(t - \frac{3}{4038})}^{2} \geq 0 \forall t \\ \Leftrightarrow {(t - \frac{3}{4038})}^{2} + \frac{2689}{2692} \geq \frac{2689}{2692} \forall t \\ \Rightarrow A \geq \frac{2689}{2692} \forall t \end{array}$

Dấu "=" xảy ra

\Leftrightarrow t = \frac{1}{1346} (t m)

Bắt đầu thi ngay