11 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 20

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 20

3253 lượt thi
11 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

a, Rút gọn biểu thức: $A = \sqrt{36} - \sqrt{4}$

Xem đáp án

a, Ta có $A = \sqrt{36} - \sqrt{4} = 6 - 2 = 4$

Câu 2:

b,Tìm x biết $\sqrt{x} = 3$

Xem đáp án

b, Điều kiện $x \geq 0$

Ta có: $\sqrt{x} = 3 \Leftrightarrow x = 3^{2} \Leftrightarrow x = 9 (t m)$

Vậy x=9

Câu 3:

Giải hệ phương trinh

\{\begin{cases} 2 x + 5 y = 12 \\ 2 x + y = 4 \end{cases}

Xem đáp án

Ta có: $\{\begin{cases} 2 x + 5 y = 12 \\ 2 x + y = 4 \end{cases} \Leftrightarrow \{\begin{cases} 4 y = 8 \\ x = \frac{4 - y}{2} \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Vậy phương trình có tập nghiệm $S = \{3; 4\}$

Câu 4:

Trong hệ trục tọa độ Oxy, cho đường thẳng $(d) : y = 6 x + b$ và parabol $(P) : y = a x^{2} (a \neq 0)$

a,Tìm giá trị của b để đường thẳng (d) đi qua điểm $M (0; 9)$

Xem đáp án

a,Đường thẳng $d : y = 6 x + b$ đi qua điểm $M (0; 9)$

$\to$ Thay $x = 0, y = 9$ vào phương trình đường thẳng $(d) : y = 6 x + b$ ta được: $9 = 6.0 + b \Leftrightarrow b = 9$ Vậy b=9

Câu 5:

b,Với b tìm được, tìm giá trị của a để (d) tiếp xúc với (P)

Xem đáp án

b,Theo câu a ta có $b = 9 \Rightarrow (d) : y = 6 x + 9$

Xét phương trình hoành độ giao điểm của đường thẳng (d) và parabol (P) ta được:

$a x^{2} = 6 x + 9 \Leftrightarrow a^{2} - 6 x - 9 = 0 (*)$

Để đường thẳng (d) tiếp xúc với parabol (P) thì phương trình (*) có nghiệm kép

$\Leftrightarrow \{\begin{cases} a \neq 0 \\ Δ' = 0 \end{cases} \Leftrightarrow \{\begin{cases} a \neq 0 \\ {(- 3)}^{2} - a . (- 9) = 0 \end{cases} \Leftrightarrow \{\begin{cases} a \neq 0 \\ a = - 1 \end{cases} \Leftrightarrow a = - 1$

Vậy a= -1 là giá trị cần tìm

Câu 6:

Cho phương trình $x^{2} - m x - 2 m^{2} + 3 m - 2 = 0$ (với m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m

Xem đáp án

Phương trình $x^{2} - m x - 2 m^{2} + 3 m - 2 = 0$ có $a = 1 \neq 0, b = - m, c = - 2 m^{2} + 3 m - 2$

Ta có: $Δ = b^{2} - 4 a c = {(- m)}^{2} - 4.1 (- 2 m^{2} + 3 m - 2) = 9 m^{2} - 12 m + 8 = {(3 m - 2)}^{2} + 4$

Vì ${(3 m - 2)}^{2} \geq 0, \forall m \Leftrightarrow {(3 m - 2)}^{2} + 4 > 0 \forall m$ hay $Δ > 0 \forall m$ nên phương trình đã cho luôn có hai nghiệm phân biệt với mọi m

Câu 7:

Chiều cao trung bình của 40 học sinh lớp 9A là 1,628m Trong đó chiều cao trung bình của học sinh nam là 1,64m và chiều cao trung bình của nữ là 1,61m Tính số học sinh nam, số học sinh nữ của lớp 9A.

Xem đáp án

Gọi số học sinh nam và số học sinh nữ của lớp 9A lần lượt là x,y $(x, y \in ℕ *, x, y < 40)$

Lớp 9A có 40 học sinh nên ta có phương trình $x + y = 40 (1)$

Vì chiều cao trung bình của học sinh lớp 9A là $1,628 m$ nên ta có phương trình:

$\frac{1,64 x + 1,61 y}{40} = 1,628 \Leftrightarrow 1,64 x + 1,61 y = 65,12 (2)$

Từ (1) và (2) ta có hệ phương trình:

$\begin{array}{l} \{\begin{cases} x + y = 40 \\ 1,64 x + 1,61 y = 65,12 \end{cases} \Leftrightarrow \{\begin{cases} y = 40 - x \\ 1,64 x + 1,61. (40 - x) = 65,12 \end{cases} \\ \Leftrightarrow \{\begin{cases} y = 40 - x \\ 1,64 x + 64,4 - 1,61 x = 65,12 \end{cases} \Leftrightarrow \{\begin{cases} y = 40 - x \\ 0,03 x = 0,72 \end{cases} \Leftrightarrow \{\begin{cases} x = 24 \\ y = 16 \end{cases} (t m) \end{array}$

Vậy lớp 9A có 24 nam, 16 nữ

Câu 8:

Người ta muốn tạo một cái khuôn đúc dạng hình trụ, có chiều cao bằng 16cm bán kính đáy bằng 8 cm, mặt đáy trên lõm xuống dạng hình nón và khoảng cách từ đỉnh hình nón đến mặt đáy dưới hình trụ bằng 10cm Tính diện tích toàn bộ khuôn (lấy $π = 3,14)$

Xem đáp án

Hình trụ có bán kính đáy r=8cm và chiều cao h=16cm nên diện tích xung quanh của hình trụ là $S_{1} = 2 π r h = 2 π .8.16 = 256 π (c m^{2})$

Diện tích 1 mặt đáy của hình trụ là $S_{2} = π r^{2} = π {.8}^{2} = 64 π (c m^{2})$

Phần hình nón bị lõm xuống có chiều cao $h_{1} = 16 - 10 = 6 c m$ và bán kính đáy $r = 8 c m .$

Đường sinh của hình nón $l = \sqrt{r^{2} + h_{1}^{2}} = \sqrt{8^{2} + 6^{2}} = 10 c m$

Diện tích xung quanh của hình nón là : $S_{3} = π r l = π .8.10 = 80 π (c m^{2})$

Diện tích toàn bộ khuôn là $S = S_{1} + S_{2} + S_{3} = 256 π + 64 π + 80 π = 400 π = 1256 (c m^{2})$

Vậy diện tích toàn bộ khuôn là $1256 (c m^{2})$

Câu 9:

Cho tam giác ABC có ba góc nhọn ( AB<AC) và đường cao $A K (K \in B C) .$ Vẽ đường tròn (O) đường kính BC. Từ A kẻ các tiếp tuyến $A M, A N$ với đường tròn (O) (với M,N là các tiếp điểm, M và B nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AO Gọi H là giao điểm của hai đường thẳng $M N, A K$

a, Chứng minh tứ giác AMKO là tứ giác nội tiếp

Xem đáp án

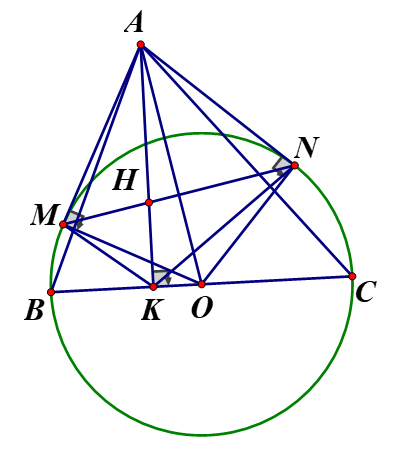
Cho tam giác ABC có ba góc nhọn ( AB<AC) và đườn cao AK ( K thuộc BC) (ảnh 1)

Xét đường tròn (O) có AM là tiếp tuyến nên $A M ⊥ O M$ hay $\hat{A M O} = 90^{0}$

Lại có: $A K ⊥ B C \Rightarrow \hat{A K O} = 90^{0}$

Xét tứ giác AMKO có $\hat{A M O} = \hat{A K O} (= 90^{0})$ nên hai đỉnh M, K kề nhau cùng nhìn cạnh AO dưới các góc vuông, do đó tứ giác AMKO là tứ giác nội tiếp.

Câu 10:

b, Chứng minh KA là tia phân giác $\hat{M K N}$

Xem đáp án

b, Xét đường tròn (O) có AN là tiếp tuyến nên $A N ⊥ O N$ hay $\hat{A N O} = 90^{0}$

Xét tứ giác KONA có $\hat{A K O} + \hat{A N O} = 90^{0} + 90^{0} = 180^{0}$ mà hai góc ở vị trí đối nhau nên KNOA là tứ giác nội tiếp $\Rightarrow \hat{N K A} = \hat{N O A} (1)$

Lại có tứ giác AMKO là tứ giác nội tiếp (cmt) $\Rightarrow \hat{M K A} = \hat{M O A} (2)$

Xét đường tròn (O) có $A M, A N$ là hai tiếp tuyến nên OA là tia phân giác của $\hat{M O N}$

Do đó $\hat{M O A} = \hat{N O A} (3)$

Từ (1), (2), (3) suy ra $\hat{M K A} = \hat{N K A}$ hay KA là tia phân giác của $\hat{M K N} (d f c m)$

Câu 11:

c, Chứng minh

A N^{2} = A K . A H

Xem đáp án

c) Xét đường tròn (O) có $\hat{A M N}$ là góc tạo bởi tiếp tuyến và dây cung MN nên $\hat{A M N} = \frac{1}{2} s d \overset{⏜}{M N} (4)$

Lại có: $\hat{M K A} = \hat{M O A} = \frac{1}{2} \hat{M O N}$ (cmt) nên $\hat{M K A} = \frac{1}{2} s d \overset{⏜}{M N} (5)$

Từ (4) , (5) suy ra $\hat{A M H} = \hat{M K A}$

Xét $Δ A M H$ và $Δ A K M$ có: $\hat{M A H}$ chung; $\hat{A M H} = \hat{M K A} (c m t)$

Nên $Δ A M H ~ Δ A K M (g . g) \Rightarrow \frac{A M}{A K} = \frac{A H}{A M} \Leftrightarrow A M^{2} = A K . A H$

Lại có: AM = AN (tính chất hai tiếp tuyến cắt nhau) $\Rightarrow A N^{2} = A K . A H (d f c m)$

Bắt đầu thi ngay